Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a:
Xét đường tròn đường kính HB có
ΔHMB nội tiếp đường tròn
HB là đường kính
Do đó: ΔHMB vuông tại M
Xét đường tròn đường kính HC có
ΔHNC nội tiếp đường tròn
HC là đường kính
Do đó: ΔHNC vuông tại N
Xét tứ giác AMHN có
\(\widehat{NAM}=\widehat{ANH}=\widehat{AMH}=90^0\)
nên AMHN là hình chữ nhật
b: \(BC=\sqrt{6^2+8^2}=10\)(cm)
=>AH=6*8/10=4,8(cm)
=>MN=4,8(cm)
c: góc EMN=góc EMH+góc NMH
=góc EHM+góc NAH
=góc HAC+góc HCA=90 độ
=>MN là tiếp tuyến của (E)

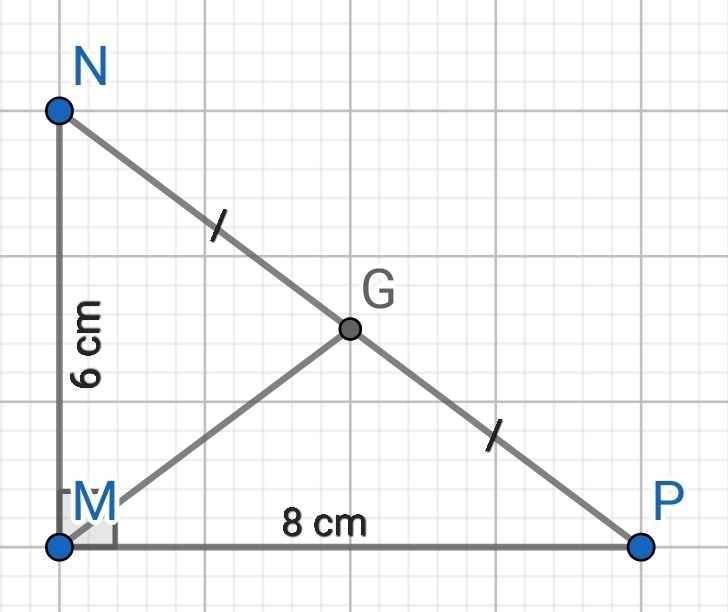
Ta có:
∆MNP vuông tại M
⇒ NP² = MP² + MN² (Pytago)
= 8² + 6² = 100
⇒ NP = 10 (cm)
Gọi G là trung điểm của NP
⇒ MG là đường trung tuyến ứng với cạnh huyền NP của ∆MNP
⇒ MG = NG = PG = NP : 2 = 5 (cm)
⇒ M, N, P cùng thuộc đường tròn tâm G, bán kính MG = 5 cm
Stshdtgfdrsgettgstgefdfe📱📱📱📱📱📱💻📱📱📱📱📱📱📱📱💻💻💻💻💻💻📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱📱🖍️🖍️📱📱📱📱📱📱📱📱📱📱💻📱💻📱💻📱💻📱💻📱💻📱💻📱💻📱💻📱📱💻💻📱💻📱💻📱💻📱📱💻💻📱📱💻📱💻📱💻📱💻📱📱💻📱📱📱📱📱📱📱💻📱💻📱📱💻📱📱📱💻📱💻📱📱📱📱📱📱💻💻💻💻📱📱📱📱
a. gọi M là trung điểm BC
△ ABC vuông tại A có AM là đường trung tuyến
\(\Rightarrow MA=MB=MC=\frac12BC\)
⇒ đường tròn có tâm M đi qua 3 đỉnh của △ ABC
độ dài cạnh BC là:
\(BC=\sqrt{AB^2+AC^2}=\sqrt{15^2+20^2}=25\left(\operatorname{cm}\right)\)
bán kính đường tròn đó là:
\(R=\frac{25}{2}=12,5\left(\operatorname{cm}\right)\)
b. gọi O là giao điểm của 2 đường chéo AC và BD
vì ABCD là hình vuông nên ta có: OA = OB = OC = OD = \(\frac12AC=\frac12BD\)
⇒ đường tròn có tâm O đi qua 4 đỉnh A,B,C,D
độ dài cạnh BD là:
\(BD=\sqrt{AD^2+AB^2}=\sqrt{12^2+12^2}=12\sqrt2\left(\operatorname{cm}\right)\)
bán kính của đường tròn đó là:
\(R=\frac{12\sqrt2}{2}=6\sqrt2\left(\operatorname{cm}\right)\)
hình câu a: