Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Thách Cao Hoàng Minh Nguyệt làm hết đống này.
làm mau.
Bài 1:
Tìm x, biết:
a)
b)
Bài 2:
Hãy tìm các tập hợp:
a) 
bài 9:
Ta có bằng:
A) 2;
B) 4;
C) 8;
D) 16.
bài 11:
Những điểm nào sau đây thuộc đồ thị hàm số y = -3x.

Bài 1:
a) 3,2.x+(−1,2).x+2,7=−4,9;3,2.x+(−1,2).x+2,7=−4,9;
(3,2−1,2)x=−4,9−2,7(3,2−1,2)x=−4,9−2,7
2.x=−7,62.x=−7,6
x=−3,8x=−3,8
b) (−5,6). x + 2,9 . x − 3,86 = −9,8 .(−5,6). x + 2,9. x−3,86 = −9,8.
(−5,6 + 2 ,9) . x = − 9.8 + 3,86 (−5,6 + 2,9) .x = −9.8 + 3,86
−2,7 .x = −5,94 − 2,7.x = −5,94
x
Giả sử x =
#Hỏi cộng đồng OLM
#Toán lớp 7

Theo đề bài ta có x = a/m, y = b/m (a, b, m ∈ Z, b # 0)
Vì x < y nên ta suy ra a < b
Ta có: x = 2a/2m, y = 2b/2m; z = (a+b)/2m
Vì a < b => a + a < a + b => 2a < a + b
Do 2a < a + b nên x < z (1)
Vì a < b => a + b < b + b => a + b < 2b
Do a + b < 2b nên z < y (2)
Từ (1) và (2) ta suy ra x < z < y
Giả sử x =
#Hỏi cộng đồng OLM
#Toán lớp 7

Theo đề bài ta có x = , y =
( a, b, m ∈ Z, m > 0)
Vì x < y nên ta suy ra a< b
Ta có : x = , y =
; z =
Vì a < b => a + a < a +b => 2a < a + b
Do 2a< a +b nên x < z (1)
Vì a < b => a + b < b + b => a + b < 2b
Do a+b < 2b nên z < y (2)
Từ (1) và (2) ta suy ra x < z< y
Theo đề bài ta có x = a/m, y = b/m (a, b, m ∈ Z, b # 0)
Vì x < y nên ta suy ra a < b
Ta có: x = 2a/2m, y = 2b/2m; z = (a+b)/2m
Vì a < b => a + a < a + b => 2a < a + b
Do 2a < a + b nên x < z (1)
Vì a < b => a + b < b + b => a + b < 2b
Do a + b < 2b nên z < y (2)
Từ (1) và (2) ta suy ra x < z < y
Giả sử x =
#Hỏi cộng đồng OLM
#Toán lớp 7

Theo đề bài ta có x = a/m, y = b/m (a, b, m ∈ Z, b # 0)
Vì x < y nên ta suy ra a < b
Ta có: x = 2a/2m, y = 2b/2m; z = (a+b)/2m
Vì a < b => a + a < a + b => 2a < a + b
Do 2a < a + b nên x < z (1)
Vì a < b => a + b < b + b => a + b < 2b
Do a + b < 2b nên z < y (2)
Từ (1) và (2) ta suy ra x < z < y

Ta thấy: \(\begin{cases}\left(x-2\right)^{2012}\ge0\\\left|y^2-9\right|^{201}\ge0\end{cases}\)
\(\Rightarrow\left(x-2\right)^{2012}+\left|y^2-9\right|^{201}\ge0\)
\(\Rightarrow\left(x-2\right)^{2012}+\left|y^2-9\right|^{201}+5\ge5\)
\(\Rightarrow A\ge5\). Dấu "=" xảy ra khi
\(\begin{cases}\left(x-2\right)^{2012}=0\\\left|y^2-9\right|^{201}=0\end{cases}\)\(\Leftrightarrow\begin{cases}x-2=0\\y^2-9=0\end{cases}\)\(\Leftrightarrow\begin{cases}x=2\\y=\pm3\end{cases}\)
Vậy \(\begin{cases}x=2\\y=\pm3\end{cases}\)

a)Ta có BIK là góc ngoài của BAI.
Nên BIK > BAI (1)
hay BIK>BAK
b) CIKCAI > ( Góc ngoài của ∆ CAI)
Từ (1) và (2) ta có:
BIK +CIK >BAI +CAI
=> BIC>BAC





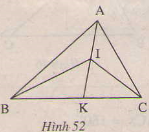
a) Ta có \(\widehat{BIK}\) là góc ngoài của \(\widehat{BAI}\)( hay là góc ngoài \(\widehat{BAK}\))
Các bạn lưu ý nếu không hiểu: Góc ngoài của tam giác lớn hơn mỗi ngóc trong không kề với nó (ở đây là tam giác ∆ BIA)
Nên \(\widehat{BIK}>\widehat{BAK}\) (1)
b) Góc \(\widehat{CIK}>\widehat{CAI}\) (Góc ngoài của ∆ CAI)
Từ (1) và (2) ta có: \(\widehat{BIK}+\widehat{CIK}>\widehat{BAK}+\widehat{CAI}\)
Mà \(\widehat{BIC}=\widehat{BIK}+\widehat{CIK};\widehat{BAC}=\widehat{BAK}+\widehat{ CAI}\)
⇒ \(\widehat{BIC}>\widehat{BAC}\)
a, Ta có góc BIK là góc ngoài của Tg BAI
=> BIK=BAK+ABI
Mà ABI>0 => BIK>BAK
b, Tương tự CIK>CAK
=> BIK+CIK>BAK+CAK
=> BIC>BAC
Chúc bạn có một ngày mới tốt lành!