Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Hình vẽ ( 1 điểm)
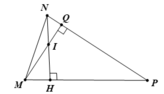
Do (MIN) là góc ngoài của tam giác MIH nên
∠(MIN) = ∠(QMH) + ∠(MHI) ( 1 điểm)
⇒∠(QMH) = ∠(MIN) - ∠(MHI) = 120o - 90o = 30o ( 1 điểm)
Trong tam giác MPQ có ∠(MPQ) + ∠(MQP) + ∠(PMQ) = 180o
Nên ∠(MPQ) = 180o - 30o - 90o = 60o ( 1 điểm)

Ta có hình vẽ sau:
M P Q N I A R
a/ Xét ΔAMQ và ΔANP có:
AM = AN (gt)
\(\widehat{MAQ}=\widehat{NAP}\) (đối đỉnh)
AQ = AP (gt)
=> ΔAMQ = ΔANP (c.g.c) (đpcm)
b/ Vì ΔAMQ = ANP (ý a)
=> \(\widehat{QMA}=\widehat{PNA}\) (2 góc tương ứng)
mà 2 góc này lại ở vị trí so le trong nên
=> MQ // PN (đpcm)
c/+) Xét ΔAMI và ΔANR có:
\(\widehat{MAI}=\widehat{NAR}\) (đối đỉnh)
AM = AN(gt)
\(\widehat{AMI}=\widehat{RNA}\) (so le trong do MQ // PN (ý b))
=> ΔAMI = ΔANR (g.c.g)
=> MI = NR (1)
+) CM tương tự ta có:
ΔAQI = ΔAPR (g.c.g)
=> QI = PR (2)
Từ (1); (2) và I là trung điểm của MQ
=> RP = RN (đpcm)


a) Ta có: \(\widehat{IOK}=\widehat{BOC}-\widehat{BOI}-\widehat{KOC}=\widehat{BOC}-60^o\)
Mà \(\widehat{BOC}=180^o-\widehat{B_1}-\widehat{C_1}=180^o-\left(\frac{\widehat{B}}{2}+\frac{\widehat{C}}{2}\right)=180^o-\frac{180^o-\widehat{A}}{2}=180^o-30^o=150^o\)
\(\Rightarrow\widehat{IOK}=150^o-60^o=90^o\Rightarrow OI\perp OK\)
b) Ta có: \(\widehat{BOE}=\widehat{COD}=180^o-30^o-90^o-30^o=30^o\)
Xét \(\Delta BEO;\Delta BIO\); có:
\(\widehat{B_1}=\widehat{B_2}\left(gt\right);\) Chung BO \(;\widehat{IOB}=\widehat{EOB}=30^o\)
=> \(\Rightarrow\Delta BEO=\Delta BIO\left(g.c.g\right)\Rightarrow BE=BI.\)
Tương tự thì KC=DC
Mà BC>BI+KC => BE > BE+DC

\(\widehat{MBA}=90^0-55^0=35^0\)
\(\widehat{MAB}=90^0-67^0=23^0\)
Do đó: \(\widehat{AMB}=122^0\)

Câu hỏi của giang ho dai ca - Toán lớp 7 - Học toán với OnlineMath
Em tham khảo tại link trên nhé.

ΔABC vuông tại A
=>\(\hat{ABC}+\hat{ACB}=90^0\)
=>\(\hat{ABC}=90^0-40^0=50^0\)
BD là phân giác của góc ABD
=>\(\hat{ABD}=\hat{DBC}=\frac12\cdot\hat{ABC}=\frac12\cdot50^0=25^0\)
Ta có: ΔBHA vuông tại H
=>\(\hat{HAB}+\hat{HBA}=90^0\)
=>\(\hat{HAB}=90^0-50^0=40^0\)
ΔBDA vuông tại A
=>\(\hat{ABD}+\hat{ADB}=90^0\)
=>\(\hat{ADB}=90^0-25^0=65^0\)
Vì B,I,D thẳng hàng nên \(\hat{BID}=180^0\)
a. Hình vẽ ( 1 điểm)
Do (MIN) là góc ngoài của tam giác MIH nên
∠(MIN) = ∠(QMH) + ∠(MHI) ( 1 điểm)
⇒∠(QMH) = ∠(MIN) - ∠(MHI) = 120o - 90o = 30o ( 1 điểm)
Trong tam giác MPQ có ∠(MPQ) + ∠(MQP) + ∠(PMQ) = 180o
Nên ∠(MPQ) = 180o - 30o - 90o = 60o ( 1 điểm)