Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Sửa đề: Xác định vị trí tương đối của các điểm A,B,C,D với đường tròn (A;4cm)
ABCD là hình vuông
=>AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm chung của AC và BD
O là trung điểm của AC
=>\(AC=2\cdot AO=2\cdot2\sqrt2=4\sqrt2\left(\operatorname{cm}\right)\)
ΔABC vuông tại B
=>\(BA^2+BC^2=AC^2\)
=>\(2\cdot AB^2=AC^2=\left(4\sqrt2\right)^2=32\)
=>\(AB^2=16=4^2\)
=>AB=4(cm)
Vì ABCD là hình vuông
nên AB=AD=4cm
=>D nằm trên (A;4cm) và B cũng nằm trên (A;4cm)
Vì AC>AB
nên C nằm ngoài (A;4cm)
🎯 Đề bài tóm tắt:
- \(A B C D\) là hình vuông
- \(O\) là giao điểm hai đường chéo → O là tâm hình vuông
- \(O A = 2 \sqrt{2} \&\text{nbsp};\text{cm}\)
- Vẽ đường tròn tâm A, bán kính 4 cm → gọi là \(\left(\right. A ; 4 \&\text{nbsp};\text{cm} \left.\right)\)
- Hỏi: Vị trí tương đối của các điểm \(A , B , C , D\) so với đường tròn \(\left(\right. O ; 4 \&\text{nbsp};\text{cm} \left.\right)\)
✳️ Bước 1: Phân tích hình vuông
Vì \(O\) là tâm hình vuông ⇒ các đoạn \(O A = O B = O C = O D\)
- Đề bài cho: \(O A = 2 \sqrt{2} \&\text{nbsp};\text{cm}\)
- Vậy \(O B = O C = O D = 2 \sqrt{2} \&\text{nbsp};\text{cm}\)
✳️ Bước 2: Xét đường tròn \(\left(\right. O ; 4 \&\text{nbsp};\text{cm} \left.\right)\)
- Đây là đường tròn tâm O, bán kính \(R = 4 \&\text{nbsp};\text{cm}\)
- Ta cần xét các điểm \(A , B , C , D\) nằm trên, trong hay ngoài đường tròn này
✅ Bước 3: So sánh các khoảng cách với bán kính 4 cm
Điểm | Khoảng cách đến O | So với bán kính 4 cm | Kết luận vị trí |
|---|---|---|---|
A | \(O A = 2 \sqrt{2} \approx 2.83 \&\text{nbsp};\text{cm}\)OA=22≈2.83 cmOA=22≈2.83 cm | < 4 cm | A nằm trong đường tròn |
B | \(O B = 2 \sqrt{2} \approx 2.83 \&\text{nbsp};\text{cm}\)OB=22≈2.83 cmOB=22≈2.83 cm | < 4 cm | B nằm trong đường tròn |
C | \(O C = 2 \sqrt{2} \approx 2.83 \&\text{nbsp};\text{cm}\)OC=22≈2.83 cmOC=22≈2.83 cm | < 4 cm | C nằm trong đường tròn |
D | \(O D = 2 \sqrt{2} \approx 2.83 \&\text{nbsp};\text{cm}\)OD=22≈2.83 cmOD=22≈2.83 cm | < 4 cm | D nằm trong đường tròn |
✍️ Kết luận cuối cùng:
Vì \(O A = O B = O C = O D = 2 \sqrt{2} < 4\), nên các điểm \(A , B , C , D\) đều nằm bên trong đường tròn \(\left(\right. O ; 4 \&\text{nbsp};\text{cm} \left.\right)\)
✅ Trả lời:
Các điểm \(A , B , C , D\) đều nằm trong đường tròn \(\left(\right. O ; 4 \&\text{nbsp};\text{cm} \left.\right)\)

1) Gọi điểm cố định là \(M\left(x_0;y_0\right)\)
\(\Leftrightarrow mx_0-m+1=y_0\) \(\left(\forall m\right)\)
\(\Leftrightarrow m\left(x_0-1\right)=y_0-1\) \(\left(\forall m\right)\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_0-1=0\\y_0-1=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x_0=1\\y_0=1\end{matrix}\right.\)
Vậy (d1) luôn đi qua điểm cố định \(\left(1;1\right)\)
2) Xét phương trình hoành độ giao điểm của (d2) và (d3)
\(2x+3=x+1\) \(\Leftrightarrow x=-2\), thay vào (d3) ta được \(y=-1\)
\(\Rightarrow\) (d3) cắt (d2) tại \(F\left(-2;-1\right)\)
Để 3 đường cắt nhau tại 1 điểm \(\Leftrightarrow F\in\left(d_1\right)\)
\(\Leftrightarrow-2m-m+1=-1\) \(\Leftrightarrow m=\dfrac{2}{3}\)
Vậy ...

A B O M N K C H I D P
Gọi KC cắt đường tròn (O) lần thứ hai tại I, BK cắt AC tại D. Kẻ đường kính IP của đường tròn (O).
Ta thấy ^IKP chắn nửa đường tròn (O) nên KP vuông góc KI. Mà KN vuông góc KI nên K,N,P thẳng hàng
Dễ dàng chứng minh \(\Delta\)IMO = \(\Delta\)PNO (c.g.c) => ^OIM = ^OPN => IM // PN hay IM // KN
Do KN vuông góc CK nên MI cũng vuông góc CK => ^MIC = ^MAC = 900 => Tứ giác ACIM nội tiếp
Suy ra ^AMC = ^AIC = ^ABK => MC // BK. Khi đó, \(\Delta\)ADB có M là trung điểm AB, MC // BD (C thuộc AD)
=> C là trung điểm AD. Nếu ta gọi BC cắt KH tại S thì \(\frac{HS}{AC}=\frac{KS}{CD}\left(=\frac{BS}{BC}\right)\)(Hệ quả ĐL Thales)
Vậy thì S là trung điểm của KH. Nói cách khác, BC chia đôi KH (tại S) (đpcm).

+ \(\left\{{}\begin{matrix}\widehat{ADC}=\widehat{ABD}\left(=\frac{1}{2}sđ\stackrel\frown{AD}của\left(O'\right)\right)\\\widehat{ACD}=\widehat{ADB}\left(=\frac{1}{2}sđ\stackrel\frown{AD}của\left(O\right)\right)\end{matrix}\right.\)
=> ΔABD ∼ ΔADC (g.g)
\(\Rightarrow\frac{AD}{AB}=\frac{AC}{AD}=\frac{CD}{BD}\)
\(\Rightarrow\frac{AD}{AB}\cdot\frac{AC}{AD}=\frac{CD^2}{BD^2}\) => đpcm

Ta có
\(AB=AC\) (Hai tiếp tuyến cùng xp từ 1 điểm thì khoảng cách từ điểm đó đến hai tiếp điểm bằng nhau)
\(\Rightarrow\Delta ABC\) cân tại A (1)
AO là phân giác của \(\widehat{BAC}\) (Hai tiếp tuyến cùng xp từ 1 điểm thì đường nối điểm đó với tâm của đường tròn là phân iacs của góc tạo bởi 2 tiếp tuyến) (2)
Từ (1) và (2) \(\Rightarrow AH\perp BC\) (Trong tg cân đường phân giác của góc ở đỉnh tg cân đồng thời là đường cao, đường trung trực...)
\(\Rightarrow\widehat{AHE}=90^o\) (*)
Ta có
\(OM=ON\) (Bán kính (O)) \(\Rightarrow\Delta OMN\) cân tại O
Ta có \(IM=IN\) (Giả thiết) => ON là đường trung tuyến của tg OMN
\(\Rightarrow OE\perp AN\) (Trong tg cân đường trung tuyến xuất phát từ đỉnh tg cân đồng thời là đường cao, đường trung trực...)
\(\Rightarrow\widehat{AIE}=90^o\) (**)
Từ (*) và (**) => I và H cùng nhìn AE dưới hai góc bằng nhau và bằng 90 độ => I và H nằm trên đường tròn đường kính AE nên 4 điểm A;H;I;E cùng nằm trên 1 đường tròn
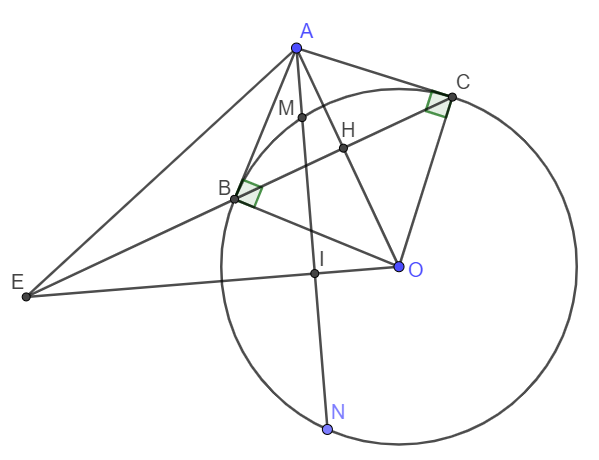
Cho đường tròn tâm OO bán kính RR và một điểm AA nằm ngoài đường tròn. Kẻ một đường thẳng đi qua AA và không đi qua OO, cắt đường tròn tại hai điểm phân biệt MM, NN (MM nằm giữa AA và NN). Từ AA vẽ hai tiếp tuyến ABAB và ACAC với (O)(O) (BB, CC là hai tiếp điểm). Đường thẳng BCBC cắt AOAO tại HH. Gọi II là trung điểm của MNMN. Đường thẳng OIOI cắt đường thẳng BCBC tại EE. Chứng minh AHIEAHIE là tứ giác nội tiếp.
theo gt, ta co:
I là trung điểm của MNMN va MN la day cung cua (O)
=> OE vuong goc voi MN tai I
hay goc AIE= 90 (1)
Mat khac, ta lai co A nam ngoai (O);
AC va AB lan luot la cac tiep tuyen cua (O)
=> AO vuong goc voi BC
hay goc AHE = 90 (2)
tu (1) va (2) => tu giac AHIE noi tiep (vi co 2 goc ke bang nhau)

a) zì H là trung điểm của AB nên \(OH\perp AB\)hay \(\widehat{OHM}=90^0\)
theo tính chất của tiếp tuyến ta lại có \(OD\perp DM\left(hay\right)\widehat{ODM}=90^0\)
=> M,D,O,H cùng nằm trên 1đường tròn
b) Theo tính chất tiếp tuyến ta có
MC=MD=> tam giác MDC cân tại M
=> MI là 1 đương phân giác của CMD , MẶt khác I là điểm chính giữa cung nhỏ CD nên :
\(\widehat{DCI}=\frac{1}{2}sđ\widebat{DI}=\frac{1}{2}sđ\widebat{CI}=\widehat{MCI}\)
=> CI là phân giác của góc MCD .
zậy I là tâm đường tròn nội tiếp tam giác MCD

C là điểm nào em nhỉ?
Bạn ơi, câu hỏi có vẻ thiếu một số thông tin hoặc có nhầm lẫn nhỏ trong phần mô tả (như “trung điểm của \(B C\)” — chưa biết điểm \(C\) ở đâu), nên mình sẽ giả sử và giải bài theo cách thông thường nhất liên quan đến đường tròn, tiếp tuyến, và trục đối xứng nhé!
Giả sử đề bài như sau:
Cho đường tròn \(\left(\right. O ; R \left.\right)\) và một đường thẳng \(x\) cắt đường tròn tại hai điểm phân biệt \(A\) và \(B\). Gọi \(y\) là đường thẳng đi qua trung điểm của đoạn thẳng \(A B\) và vuông góc với \(A B\).
Chứng minh: Đường thẳng \(y\) là trục đối xứng của đường tròn \(\left(\right. O \left.\right)\).
Lời giải:
\(O A = O B = R\)
Kết luận: