Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có : BC = BH + HC = 9 + 16 = 25 (cm)
Tam giác ABC vuông tại A nên :
BC2 = AB2 + AC2
252 = AB2 + 162
=> AB2 = 252 - 202
AB2 = 625 - 400 = 225 = 152
=> AB = 15 (cm)
Tam giác AHC vuông tại H nên :
AC2 = AH2 + HC2
202 = AH2 + 162
=> AH2 = 202 - 162
AH = 400 - 256 = 144 = 122
=> AH = 12 (cm)
Vậy AB = 15 cm ; AH = 12 cm
Tham khảo link này nek:
https://h.vn/hoi-dap/question/168012.html
# mui #

a)\(\Delta ABH\) vuông tại H có:
BH2 =AB2 -AH2 =132 -122 =25( ĐL Pytago)
=> BH=5 cm
BC=BH+HC=5+16=21 cm
\(\Delta AHC\) vuông tại H có:
AH2 + HC2 =AC2 ( đl Pytago)
=> AC2 =122 + 162 =20 cm
b) \(\Delta AHB\) vuông tại H có: AB2 = AH2 +BH2 ( ĐL Pytago)
=> BH2 =AB2 - AH2 =132 - 122 =25
=> BH=5 cm
BC= BH+HC=5+16=21 cm
\(\Delta AHC\) vuông tại H có: AC2 = AH2 +HC2 ( đL Pytago)
=> AC2 = 122 + 162 =400
=> AC= 20 cm

Áp dụng định lý Pitago:
$AC=\sqrt{BC^2-AB^2}=\sqrt{13^2-5^2}=12$ (cm)
$AH=\frac{2S_{ABC}}{BC}=\frac{AB.AC}{BC}=\frac{5.12}{13}=\frac{60}{13}$ (cm)
$CH=\sqrt{AC^2-AH^2}=\sqrt{12^2-(\frac{60}{13})^2}=\frac{144}{13}$ (cm)
$BH=BC-CH=13-\frac{144}{13}=\frac{25}{13}$ (cm)
- Áp dụng định lý pi ta go vào tam giác ABC vuông tại A ta được :
\(AB^2+AC^2=BC^2\)
\(\Rightarrow AC^2+5^2=13^2\)
\(\Rightarrow AC=12\left(cm\right)\)
- Xét tam giác BHA và tam giác BAC có : \(\left\{{}\begin{matrix}\widehat{BHA}=\widehat{BAC}=90^o\\\widehat{B}\left(chung\right)\end{matrix}\right.\)
=> Hai tam giác trên đồng dạng .
=> \(\dfrac{BH}{AB}=\dfrac{AB}{BC}\)
=> \(BH=\dfrac{AB^2}{BC}=\dfrac{25}{13}\left(cm\right)\)
=> \(CH=BC-BH=\dfrac{144}{13}\left(cm\right)\)
- Áp dụng định lý pi ta go vào tam giác ABH vuông tại H ta được :
\(AH^2+BH^2=AB^2\)
\(\Rightarrow AH=\dfrac{60}{13}\left(cm\right)\)

ABCH??20cm16 cm9 cm
Lg
*Áp dụng định lý py-ta-go ta có: (Δ AHC)
AC2=AH2+HC2
202=AH2+162
400=AH2+256
AH2=144
AH=√144 =12
*Áp dụng định lý py-ta-go ta có: (Δ AHB)
AB2=AH2+BH2
AB2=122+92
AB2=225
AB=√225 =15

a: Xét ΔBAD và ΔBED có
BA=BE
\(\hat{ABD}=\hat{EBD}\) (BD là phân giác của góc ABE)
BD chung
Do đó: ΔBAD=ΔBED
=>DA=DE
b: ΔBAD=ΔBED
=>\(\hat{BAD}=\hat{BED}\)
=>\(\hat{BED}=90^0\)
=>DE⊥BC
mà AH⊥BC
nên DE//AH
c: Xét ΔMHA và ΔMDK có
MH=MD
\(\hat{MHA}=\hat{MDK}\) (hai góc so le trong, HA//DK)
HA=DK
Do đó: ΔMHA=ΔMDK
=>\(\hat{HMA}=\hat{DMK}\)
mà \(\hat{HMA}+\hat{AMD}=180^0\) (hai góc kề bù)
nên \(\hat{AMD}+\hat{DMK}=180^0\)
=>A,M,K thẳng hàng
Chúng ta sẽ giải từng câu hỏi trong bài toán này.
Câu a) Chứng minh ∆ABD = ∆EBD và AD = ED
- Điều kiện:
- ∆ABC vuông tại A (AB < AC).
- Tia phân giác của góc B cắt AC tại D.
- Trên cạnh BC lấy điểm E sao cho BE = BA.
- Vẽ AH BC tại H.
- Chứng minh:
- Xét các tam giác ∆ABD và ∆EBD:
Vậy, theo Tiêu chuẩn góc-cạnh-góc (Axiom SAS), ta có:
\(\Delta A B D = \Delta E B D\) - Cả hai tam giác ∆ABD và ∆EBD có cạnh chung BD.
- AB = BE (do đề bài cho BE = BA).
- Góc ABD = Góc EBD (vì tia BD là tia phân giác của góc ABC, nên hai góc này bằng nhau).
- Kết luận AD = ED:
- Do ∆ABD = ∆EBD (theo chứng minh trên), nên các cạnh tương ứng của hai tam giác này cũng bằng nhau.
- Vậy, AD = ED.
Câu b) Chứng minh AH // DE
- Xét đoạn AH và DE:
- Từ điều kiện bài toán, chúng ta có điểm H là giao điểm của đường vuông góc AH với cạnh BC, tức là AH ⊥ BC.
- Tia DE được dựng sao cho DE là một đoạn thẳng trong cùng một mặt phẳng với BC, và điểm D là điểm phân giác của góc B.
- Chứng minh AH // DE:
- Vì ∆ABD = ∆EBD (chứng minh ở câu a) nên các góc tương ứng của hai tam giác này cũng bằng nhau. Đặc biệt, ∠BAD = ∠BED.
- Ta có AH ⊥ BC và ∠BAD = ∠BED. Do đó, theo tính chất của góc tạo thành giữa đường vuông góc và đoạn thẳng, ta suy ra rằng AH // DE.
Câu c) Chứng minh A, M, K thẳng hàng
- Định nghĩa các điểm:
- Trên tia DE, lấy điểm K sao cho DK = AH.
- M là trung điểm của DH, tức là:
\(\text{DM} = \text{MH}\)
- Chứng minh A, M, K thẳng hàng:
- Ta đã biết rằng AH // DE, và từ câu b) đã chứng minh rằng AH và DE song song.
- M là trung điểm của DH, tức là DM = MH. Đồng thời, ta có DK = AH (theo giả thiết).
- Vì AH // DE và M là trung điểm của DH, ta có thể sử dụng tính chất của các đường trung tuyến trong tam giác vuông để suy ra rằng các điểm A, M, K nằm trên cùng một đường thẳng.
Kết luận:
- a) ∆ABD = ∆EBD và AD = ED.
- b) AH // DE.
- c) A, M, K thẳng hàng.
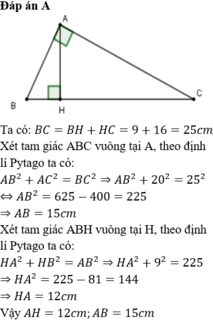
Ta có: BC = HB+HC = 9+16=25cm
Áp dụng định lý pitago vào tam giác vuông ABC, có:
\(BC^2=AB^2+AC^2\)
\(\Rightarrow AB=\sqrt{BC^2-AC^2}=\sqrt{25^2-20^2}=\sqrt{225}=15cm\)
Áp dụng định lý pitago vào tam giác vuông ABH, có:
\(AB^2=AH^2+BH^2\)
\(\Rightarrow AH=\sqrt{AB^2-BH^2}=\sqrt{15^2-9^2}=\sqrt{144}=12cm\)
\(BC=BH+HC\)
\(\Rightarrow BC=9cm+16cm=25\left(cm\right)\)
\(\text{Xét }\Delta ABC\text{ vuông tại }A\text{ có:}\)
\(BC^2=AB^2+AC^2\)
\(\Rightarrow AB^2=BC^2-AC^2\text{(định lí Py ta go đảo)}\)
\(\Rightarrow AB^2=25^2-20^2=625-400=225\left(cm\right)\)
\(\Rightarrow AB=\sqrt{225}=15\left(cm\right)\)
\(\text{Xét }\Delta AHC\text{ vuông tại }H\text{ có:}\)
\(AC^2=AH^2+HC^2\)
\(\Rightarrow AH^2-AC^2-HC^2\text{(định lí Py ta go đảo)}\)
\(\Rightarrow AH^2=20^2-16^2=400-256=144\left(cm\right)\)
\(\Rightarrow AH=\sqrt{144}=12\left(cm\right)\)