Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đề nghị bạn gửi mỗi bài một câu thôi, nhìn thế này hoa mắt quá :)
1. Chu kì sóng: \(T=\frac{2\pi}{\omega}=\frac{2\pi}{4\pi}=0,5s\)
Bước sóng: \(\lambda=v.T=12.0,5=6m\)
Độ lệch pha giữa 2 điểm: \(\Delta\varphi=\frac{2\pi d}{\lambda}=\frac{2\pi.1,5}{6}=\frac{\pi}{2}\)

Phương trình sóng tổng quát :\(u=a\cos(wt-2\pi\frac{x}{\lambda})\)
\(u=28\cos(2000t-20x)(cm)\)
So sánh với phương trình sóng bài cho
\(w=2000 (rad/s)\Rightarrow f = \frac{1000}{\pi} ,\\ 2\pi\frac{x}{\lambda}= 20x \Rightarrow \lambda = \frac{\pi}{10}(m)\Rightarrow v = \lambda.f= 100m/s. \)

Hướng dẫn: Chọn đáp án A
Chú ý: Nếu phương trình dao động tại nguồn u = A cos ω t + β thì phương trình sóng tại M cách O một khoảng x là
u = A cos ω t + β − 2 π λ x .
1) Vận tốc dao động của phần tử vật chất tại điểm M là đạo hàm của li độ theo t:
v
=
u
t
'
=
−
ω
A
sin
ω
t
+
β
−
2
π
λ
x
2) Hệ số góc của tiếp tuyến với đường sin tại điểm M là đạo hàm li độ theo x:
tan α = u x ' = 2 π λ A sin ω t + β − 2 π λ x

Đáp án: A
HD Giải: v = H e _ s o _ t r u o c _ t H e _ s o _ t r u o c _ x = 20 4 = 5 m / s

Đáp án C
Từ phương trình ta có λ = 3m; f = 50Hz => v = λf = 3.50 = 150 m/s
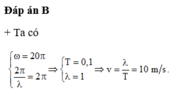
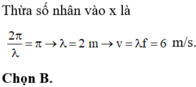
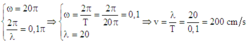
1. Độ lệch pha giữa A và M: \(\Delta\varphi=\frac{2\pi d}{\lambda}\)
M ngược pha với A khi: \(\Delta\varphi=\left(2k+1\right)\pi\Leftrightarrow\frac{2\pi d}{\lambda}=\left(2k+1\right)\pi\Leftrightarrow d=\left(k+0,5\right)\lambda\)
2. \(u=8\sin\left(\pi^2x-8\pi^2t\right)\)
Suy ra: \(\begin{cases}T=\frac{2\pi}{8\pi^2}=\frac{1}{4\pi}\\\pi^2x=\frac{2\pi x}{\lambda}\end{cases}\Leftrightarrow\begin{cases}T=\frac{1}{4\pi}\\\lambda=\frac{2}{\pi}\end{cases}\)
Vậy \(v=\frac{\lambda}{T}=8\)(m/s)