write apassage about 60-80 words about afestival
-what festival is it?
-when do you celebrate it?
-what activities does your family do?
-what food does your family eat?
do you like the festival?why or why not?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

5\(^{2x-1}\) = 5\(^{2x-3}\) + 125.24
5\(^{2x-1}\) - 5\(^{2x-3}\) = 125.24
\(5^{2x-3}\).(\(5^2\) - 1) = 125.24
\(5^{2x-3}\) .(25- 1) = 125.24
\(5^{2x-3}\). 24 = 125.24
\(5^{2x-3}\) = 125.(24:24)
\(5^{2x-3}\) = 125
\(5^{2x-3}\) = \(5^3\)
2\(x\) - 3 = 3
2\(x\) = 3 + 3
2\(x\) = 6
\(x=6:2\)
\(x=3\)
Vậy \(x=3\)
Ta có: 5^(2x-1) = 5^(2x-3) + 125.24
=> 5^2x : 5 = 5^2x : 5^3 + 3000
=> 5^2x . 1/5 = 5^2x . 1/125 + 3000
=> 5^2x . 1/5 - 5^2x . 1/125 = 3000
=> 5^2x . (1/5 - 1/125) = 3000
=> 5^2x . 24/125 = 3000
=> 5^2x = 3000 : 24/125
=> 5^2x = 15625
=> 5^2x = 5^6
=> 2x = 6
=> x = 3

Gọi số tiền của 3 bạn Nam, Thư, Sinh lần lượt là: \(x,y,z\) ( đồng\(;x,y,z>0\))
Theo bào ra, ta có:
\(\dfrac{x}{6}=\dfrac{y}{7}=\dfrac{z}{8}\) và \(x+y+z=168000\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\dfrac{x}{6}=\dfrac{y}{7}=\dfrac{z}{8}=\dfrac{x+y+z}{6+7+8}=\dfrac{168000}{21}=8000\)
Do đó:
\(\dfrac{x}{6}=8000\) nên \(x=8000.6=48000\)
\(\dfrac{y}{7}=8000\) nên \(y=8000.7=56000\)
\(\dfrac{z}{8}=8000\) nên \(z=8000.8=64000\)
Vậy số tiền của 3 bạn Nam, Thư, Sinh lần lượt là \(48000\) đồng; \(56000\) đồng; \(64000\) đồng

a: Xét ΔEDG và ΔFDG có
DE=DF
DG chung
EG=FG
Do đó: ΔEDG=ΔFDG
=>\(\widehat{EDG}=\widehat{FDG}\)
=>DG là phân giác của góc EDF
=>\(\widehat{EDG}=\dfrac{90^0}{2}=45^0=\widehat{DFG}\)
b:
Ta có: ΔDEF cân tại D
mà DG là đường trung tuyến
nên DG\(\perp\)EF tại G
Ta có: \(\widehat{IDE}+\widehat{IDF}=\widehat{EDF}=90^0\)
\(\widehat{IDF}+\widehat{DFK}=90^0\)(ΔFKD vuông tại K)
Do đó: \(\widehat{IDE}=\widehat{DFK}\)
Xét ΔIDE vuông tại I và ΔKFD vuông tại K có
DE=FD
\(\widehat{IDE}=\widehat{KFD}\)
Do đó: ΔIDE=ΔKFD
=>EI=DK
Xét tứ giác FGKD có \(\widehat{FKD}=\widehat{FGD}=90^0\)
nên FGKD là tứ giác nội tiếp
=>\(\widehat{GKH}=\widehat{GFD}\left(=180^0-\widehat{GKD}\right)\)
=>\(\widehat{GKH}=45^0\)
Xét tứ giác DGIE có \(\widehat{DGE}=\widehat{DIE}=90^0\)
nên DGIE là tứ giác nội tiếp
=>\(\widehat{GID}=\widehat{GED}=45^0\)
Xét ΔGIK có \(\widehat{GIK}=\widehat{GKI}=45^0\)
nên ΔGIK vuông cân tại G

x;y;z tỉ lệ với 3;5;6
=>\(\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{z}{6}\)
mà 3x+y-z=-52
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{z}{6}=\dfrac{3x+y-z}{3\cdot3+5-6}=\dfrac{-52}{9+5-6}=\dfrac{-52}{8}=-\dfrac{13}{2}\)
=>\(\left\{{}\begin{matrix}x=-\dfrac{13}{2}\cdot3=-\dfrac{39}{2}\\y=-\dfrac{13}{2}\cdot5=-\dfrac{65}{2}\\z=-\dfrac{13}{2}\cdot6=-39\end{matrix}\right.\)

a: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
Do đó: ΔAMB=ΔAMC
b: ΔAMB=ΔAMC
=>\(\widehat{MAB}=\widehat{MAC}\)
Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
\(\widehat{EAM}=\widehat{FAM}\)
Do đó: ΔAEM=ΔAFM
=>ME=MF
mà MF<MC(ΔMFC vuông tại F)
nên ME<MC

1. Vẽ hình:
- Vẽ tam giác ABC cân tại A (AB = AC).
- Vẽ tia phân giác góc A, cắt cạnh BC tại điểm H.
- Từ điểm H, vẽ đường vuông góc xuống cạnh AB tại điểm K (HK là hình chiếu của H trên AB).
- Từ điểm H, vẽ đường vuông góc xuống cạnh AC tại điểm M (HM là hình chiếu của H trên AC).
2. Phân tích bài toán:
- Vì tam giác ABC cân tại A, nên góc B = góc C.
- Vì AH là tia phân giác góc A, nên góc BAH = góc CAH.
- HK và HM là các đường cao, tạo ra các tam giác vuông HKH và HCM.
3. Các tính chất và định lý có thể áp dụng:
- Tính chất của tam giác cân: Hai góc ở đáy bằng nhau, đường phân giác cũng là đường trung tuyến, đường cao.
- Định lý về các trường hợp bằng nhau của tam giác vuông.
- Tính chất của tia phân giác trong tam giác.
4. Một số điều có thể chứng minh được từ bài toán:
- Tam giác AHK bằng tam giác AHM (cạnh huyền - góc nhọn).
- HK=HM.
- Tam giác BKH bằng tam giác CHM(cạnh huyền-góc nhọn).
- BK=CM.
- BH=CH.
Hình vẽ minh họa:
A
/ \
/ \
/ \
K-------M
/ \ / \
B---H---C
Lưu ý:
- Hình vẽ chỉ mang tính chất minh họa, bạn nên tự vẽ hình chính xác để dễ dàng quan sát và giải bài toán.
- Bạn có thể sử dụng các tính chất và định lý đã nêu để chứng minh các điều cần thiết trong bài toán.

a/ Tính góc MAN:
- Vì tam giác ABN cân tại B (BA=BN) và tam giác ACM cân tại C (CA=CM) nên:
- Góc ANB = (180° - góc ABC) / 2
- Góc AMC = (180° - góc ACB) / 2
- Trong tam giác ABC vuông tại A, ta có: góc ABC + góc ACB = 90°
- Suy ra: góc ANB + góc AMC = (360° - (góc ABC + góc ACB)) / 2 = (360° - 90°) / 2 = 135°
- Trong tam giác AMN, ta có: góc MAN = 180° - (góc ANB + góc AMC) = 180° - 135° = 45°
b/ Chứng minh MD vuông góc với AN, NE vuông góc với AM:
- Xét tam giác ABN cân tại B, tia phân giác góc ABC cắt AN tại D nên D là trung điểm của AN.
- Xét tam giác ACM cân tại C, tia phân giác góc ACB cắt AM tại E nên E là trung điểm của AM.
- Xét tam giác AMN, ta có:
- MD là đường trung tuyến của cạnh AN.
- NE là đường trung tuyến của cạnh AM.
- Gọi O là giao điểm của MD và AN.
- Xét tam giác ADN, ta có:
- AD = DN (D là trung điểm AN)
- MD là đường trung tuyến.
- Tam giác ADN cân tại D.
- Suy ra: MD vuông góc với AN.
- Tương tự, ta chứng minh được NE vuông góc với AM.
c/ Chứng minh tam giác IEK vuông cân:
- Gọi I là trung điểm của MN.
- Ta có:
- ID là đường trung bình của tam giác AMN.
- IE là đường trung bình của tam giác AMN.
- Suy ra: ID // AM và IE // AN.
- Mà AM vuông góc với NE và AN vuông góc với MD nên ID vuông góc với NE và IE vuông góc với MD.
- Xét tứ giác MDNE, ta có:
- Góc MDN = góc MEN = 90°
- Suy ra: tứ giác MDNE nội tiếp.
- Gọi H là giao điểm của MD và NE.
- Xét tam giác AHN vuông tại H, ta có: K là trung điểm của AH nên KH = KA = KN.
- Xét tam giác AMH vuông tại H, ta có: K là trung điểm của AH nên KH = KA = KM.
- Suy ra: KN = KM.
- Xét tam giác KMN, ta có: KN = KM và I là trung điểm của MN nên KI vuông góc với MN.
- Xét tam giác IEK, ta có:
- IE vuông góc với MD.
- KI vuông góc với MN.
- Suy ra: tam giác IEK vuông tại I.
- Xét tam giác KMN cân tại K, ta có: góc KMN = góc KNM.
- Mà góc KMN = góc IEK và góc KNM = góc IKE nên góc IEK = góc IKE.
- Suy ra: tam giác IEK cân tại I.
- Vậy tam giác IEK vuông cân tại I.

Gọi số học sinh vụn ba lớp 7A,7B,7C tham gia lần lượt là a,b,c
(Điều kiện: a>0; b>0; c>0; a,b,c\(\in\)Z)
Vì số học sinh của ba lớp 7A,7B,7C tham gia lần lượt tỉ lệ với 8;9;10
=>\(\dfrac{a}{8}=\dfrac{b}{9}=\dfrac{c}{10}\)
1. Đặt biến:
- Gọi số học sinh tham gia hoạt động của lớp 7A là x.
- Gọi số học sinh tham gia hoạt động của lớp 7B là y.
- Gọi số học sinh tham gia hoạt động của lớp 7C là z.
2. Lập tỉ lệ thức:
- Theo đề bài, số học sinh của ba lớp 7A, 7B, 7C tham gia hoạt động tỉ lệ với 8, 9, 10. Ta có tỉ lệ thức:
- x/8 = y/9 = z/10
3. Kết luận:
- Dãy tỉ số bằng nhau x/8 = y/9 = z/10 thể hiện mối quan hệ về số học sinh tham gia hoạt động giữa ba lớp 7A, 7B và 7C.
- Nếu bạn biết tổng số học sinh tham gia hoạt động của cả ba lớp, bạn có thể áp dụng tính chất của dãy tỉ số bằng nhau để tìm số học sinh cụ thể của từng lớp.
Ví dụ bổ sung:
Giả sử tổng số học sinh của cả ba lớp tham gia hoạt động là 81 em. Ta có thể giải như sau:
- Áp dụng tính chất của dãy tỉ số bằng nhau:
- x/8 = y/9 = z/10 = (x + y + z) / (8 + 9 + 10) = 81 / 27 = 3
- Từ đó, ta tìm được:
- x = 8 * 3 = 24 (học sinh)
- y = 9 * 3 = 27 (học sinh)
- z = 10 * 3 = 30 (học sinh)
Vậy số học sinh tham gia hoạt động của các lớp 7A, 7B, 7C lần lượt là 24, 27 và 30 em.

Để chứng minh rằng \(\angle A F B < \angle A F C\) trong tam giác \(A B C\), với \(A B < A C\) và \(F\) là trung điểm của \(B C\), chúng ta sẽ sử dụng một số tính chất của tam giác và góc.
Đề bài:
- Tam giác \(A B C\) có \(A B < A C\).
- \(F\) là trung điểm của \(B C\).
- Chứng minh rằng \(\angle A F B < \angle A F C\).
Lời giải:
Bước 1: Sử dụng tính chất đối xứng của tam giác
Vì \(F\) là trung điểm của \(B C\), ta có \(B F = F C\). Bây giờ, ta sẽ phân tích hai góc \(\angle A F B\) và \(\angle A F C\).
- Góc \(\angle A F B\) và \(\angle A F C\) có chung một cạnh là đoạn \(A F\) và một điểm chung là \(F\).
- Vì \(A B < A C\), ta biết rằng \(A\) gần \(B\) hơn so với \(C\). Điều này sẽ ảnh hưởng đến giá trị của các góc \(\angle A F B\) và \(\angle A F C\).
Bước 2: Tính chất của các góc trong tam giác
- Trong tam giác \(A B C\), góc \(\angle A F B\) và \(\angle A F C\) là góc ngoài tại các đỉnh \(B\) và \(C\) của tam giác \(A B C\). Theo định lý góc ngoài, góc ngoài tại một đỉnh của tam giác luôn lớn hơn góc trong cùng phía của tam giác.
Bước 3: Sử dụng định lý so sánh góc
Vì \(A B < A C\), ta có thể kết luận rằng góc \(\angle A F B\) sẽ nhỏ hơn góc \(\angle A F C\). Điều này là do góc đối diện với đoạn \(A B\) (góc \(\angle A F B\)) sẽ nhỏ hơn góc đối diện với đoạn \(A C\) (góc \(\angle A F C\)) trong tam giác.
Kết luận:
Vậy, \(\angle A F B < \angle A F C\) khi \(A B < A C\) và \(F\) là trung điểm của \(B C\), theo các tính chất hình học về góc và đối xứng trong tam giác.
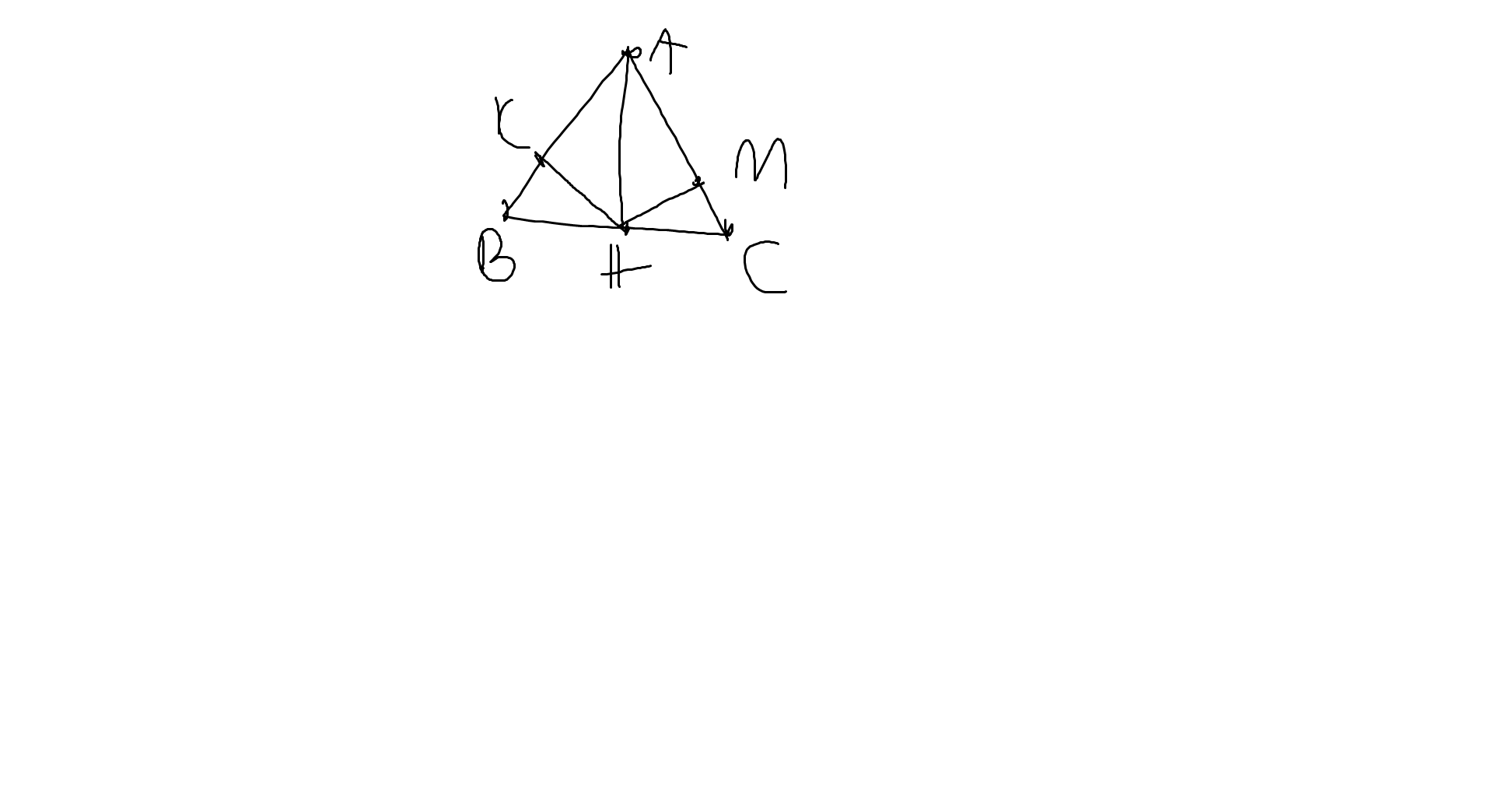
Thanksgiving, celebrated on the fourth Thursday of November, is a special occasion to express gratitude for the harvest and blessings of the year. My family gathers around the table to share a feast featuring roasted turkey, stuffing, cranberry sauce, and pumpkin pie. We also take time to reflect on what we’re thankful for and enjoy games together. I cherish Thanksgiving because it strengthens our family bond and reminds us to appreciate the little things in life!
One of my favorite festivals is Tet, which is the Vietnamese Lunar New Year celebrated in late January or early February. During Tet, my family prepares special foods like sticky rice cakes and sweet treats. We also decorate our home with flowers and orange trees to invite good luck. On New Year's Eve, we gather to enjoy a big family meal, share gifts, and remember our ancestors. I really enjoy Tet because it brings joy and togetherness, marking a fresh start for everyone.