Một ngọn núi dạng hình nón có độ dài sườn núi là 600m, bán kính của đường tròn đáy là 200m. Nếu làm một con đường có độ dài nhỏ nhất xuất phát từ một điểm A nằm ở chân núi, đi vòng quanh núi và tới điểm B là điểm nằm trên đoạn thẳng nối A và đỉnh núi sao cho \(AB=100m\) thì con đường này ban đầu sẽ đi lên dốc nhưng lúc sau sẽ đi xuống dốc. Hỏi độ dài đoạn...
Đọc tiếp
Một ngọn núi dạng hình nón có độ dài sườn núi là 600m, bán kính của đường tròn đáy là 200m. Nếu làm một con đường có độ dài nhỏ nhất xuất phát từ một điểm A nằm ở chân núi, đi vòng quanh núi và tới điểm B là điểm nằm trên đoạn thẳng nối A và đỉnh núi sao cho \(AB=100m\) thì con đường này ban đầu sẽ đi lên dốc nhưng lúc sau sẽ đi xuống dốc. Hỏi độ dài đoạn đường xuống dốc là bao nhiêu?
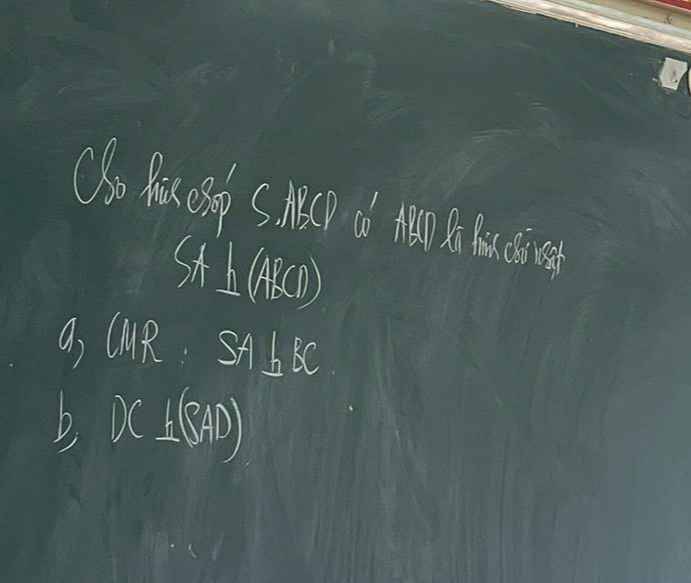
Cắt hình nón theo đường sinh OA và trải ra mặt phẳng ta đương hình quạt như hình vẽ sau
Ta có góc ở đỉnh của hình quạt là \(\dfrac{2\pi\cdot200}{600}=\dfrac{2\pi}{3}\)
Lại có, con đường từ A đến B ngắn nhất => AB là đoạn thẳng
Từ đó, đỉnh dốc H cao nhất nên gần đỉnh O => H là hình chiếu vuông góc của O lên AB
Áp dụng định lý cosin trong tam giác OAB ta có:
\(AB=\sqrt{OA^2+OB^2-2OA.OB.cos\left(\dfrac{2\pi}{3}\right)}=10\sqrt{91}\)
\(cosOBA=\dfrac{OB^2+BA^2-OA^2}{2\cdot OB\cdot OA}\)
\(HB=OB.cosOBH=OB.\left(\dfrac{OB^2+BA^2-ÓA^2}{2\cdot OA\cdot OB}\right)=\dfrac{400}{\sqrt{91}}\)Vậy quãng đường xuống dốc là \(HB=\dfrac{400}{\sqrt{91}}\)