Xét dấu f(x) = x2 - 4x -12
help me
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
15 tháng 4 2018
Đáp án: B
Ta có bảng xét dấu:
Dựa vào bảng xét dấu ta thấy: f(x) > 0 khi x < -7 hoặc -1 < x < 1 hoặc x > 3
17 tháng 2 2022
b: \(\Delta=2^2-4\cdot1\cdot1=0\)
Do đó: Tam thức này dương khi x khác -1; bằng 0 khi x=-1
a: \(\Delta=3^2-4\cdot\left(-5\right)\cdot\left(-1\right)=9-20=-11< 0\)
Do đó: Tam thức này luôn âm với mọi x
c: \(\Delta=1^2-4\cdot1\cdot\left(-2\right)=9\)
Do đó: Tam thức này âm khi -2<x<1
Bằng 0 khi x=-2 hoặc x=1
Dương khi x<-2 hoặc x>1
PT
1
CM
7 tháng 4 2017
f(x) = x2 – 5x +4
f(4)= 0; f(2) = -2 < 0; f(-1)= 10 > 0; f(0) = 4 > 0
13 tháng 1 2023
Đặt f(x)=0
=>5x^2+4x-1=0
=>(x+1)(5x-1)=0
=>x=-1 hoặc x=1/5
=>f(x)<0 khi -1<x<1/5 và f(x)>0 khi x<-1 hoặc x>1/5
CM
3 tháng 5 2018
Chọn A
Ta có –x2+x-1= 0 vô nghiệm,
6x2- 5x+1= 0 khi x= ½ hoặc x= 1/3
Bảng xét dấu
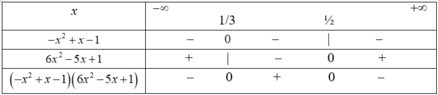
Suy ra f(x) > 0 khi và chỉ khi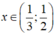 
Và f( x)< 0 khi và chỉ khi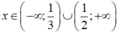 
10 tháng 3 2022
\(f\left(x\right)=\dfrac{11x+3}{-x^2+5x-7}.\)
Ta có: \(-x^2+5x-7\) là 1 tam thức bậc 2.
\(\left\{{}\begin{matrix}a=-1< 0.\\\Delta=5^2-4.\left(-1\right).\left(-7\right)=-3< 0.\end{matrix}\right.\)
\(\Rightarrow-x^2+5x-7>0\forall x\in R.\)
\(\Rightarrow\) \(f\left(x\right)>0.\Leftrightarrow11x+3>0.\Leftrightarrow x>\dfrac{-3}{11}.\\ f\left(x\right)< 0.\Leftrightarrow11x+3>0.\Leftrightarrow x>\dfrac{-3}{11}.\\ f\left(x\right)=0.\Leftrightarrow x=\dfrac{-3}{11}.\)
PT
1
CM
21 tháng 6 2017
f(x) = (3x2 – 4x)(2x2 – x – 1)
+ Tam thức 3x2 – 4x có hai nghiệm x = 0 và x = 4/3, hệ số a = 3 > 0.
Do đó 3x2 – 4x mang dấu + khi x < 0 hoặc x > 4/3 và mang dấu – khi 0 < x < 4/3.
+ Tam thức 2x2 – x – 1 có hai nghiệm x = –1/2 và x = 1, hệ số a = 2 > 0
Do đó 2x2 – x – 1 mang dấu + khi x < –1/2 hoặc x > 1 và mang dấu – khi –1/2 < x < 1.
Ta có bảng xét dấu:
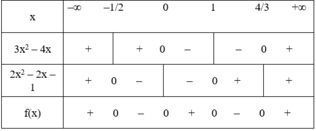
Kết luận:
f(x) > 0 ⇔ x ∈ (–∞; –1/2) ∪ (0; 1) ∪ (4/3; +∞)
f(x) = 0 ⇔ x ∈ {–1/2; 0; 1; 4/3}
f(x) < 0 ⇔ x ∈ (–1/2; 0) ∪ (1; 4/3)
Em làm nhưng không chắc đúng phần này em mới học ạ
help me pls