- tìm số nguyên x biết : x+1 trên 2 =36 phan x
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NM
8
Những câu hỏi liên quan
LN
2
31 tháng 12 2021
=>-(1+2+...+x)=-36
=>1+2+...+x=36
\(\Leftrightarrow x=8\)
PT
2
CM
4 tháng 7 2018
a) {-2).x = -10 => x = (-10): (- 2) => x = 5.
b) (-18). x = -36 => x = (-36): (-18) => x = 2.
c) 2.x + 1 = 3=>2x = 2 => x = l.
d) (-4).x + 5 = -15 => (-4)x = (-15) -5 => (-4) x = -20 => x = 5.
NV
25 tháng 8 2022
a) {-2).x = -10 => x = (-10): (- 2) => x = 5.
b) (-18). x = -36 => x = (-36): (-18) => x = 2.
c) 2.x + 1 = 3=>2x = 2 => x = l.
d) (-4).x + 5 = -15 => (-4)x = (-15) -5 => (-4) x = -20 => x = 5.
TD
2 tháng 2 2017
1. x + 2x = -36
=> 3x = -36
=> x = -36 : 3
=> x = -12
2. (2x + 3) \(⋮\)(x - 2)
=> (2x - 2) + 5 \(⋮\)(x - 2)
=> 2(x - 2) + 5 \(⋮\)(x - 2)
=> 5 \(⋮\)(x - 2)
=> x - 2 \(\in\)Ư(5) = {-5;-1;1;5}
=> x \(\in\){-3;1;3;7}
3. Khi đó a . (-b) = -132
4. -2(3x + 2) = 12 + 22 + 32
=> -2(3x + 2) = 1 + 4 + 9
=> -2(3x + 2) = 14
=> 3x + 2 = 14 : (-2)
=> 3x+ 2 = -7
=> 3x = -7 - 2
=> 3x = -9
=> x = -9 : 3
=> x = -3
LH
2 tháng 2 2017
1/ \(x+2x=-36\)
\(\Rightarrow3x=-36\)
\(\Rightarrow x=-\frac{36}{3}\)
\(\Rightarrow x=-12\)
2/ \(\left(2x+3\right)⋮\left(x-2\right)\)
\(\Leftrightarrow\left(2x-4\right)+7⋮\left(x-2\right)\)
\(\Leftrightarrow2\left(x-2\right)+7⋮\left(x-2\right)\)
\(\Rightarrow7⋮\left(x-2\right)\)
\(\Rightarrow\left(x-2\right)\inƯ\left(7\right)\)
\(\Rightarrow x\inƯ\left(7-2\right)\)
\(\Rightarrow x\inƯ\left(5\right)\)
\(\Rightarrow x\in\left\{-5,1,5\right\}\)
Vậy x nhỏ nhất để \(\left(2x-3\right)⋮\left(x-2\right)\) là -5
3/ Vì \(a\cdot b=32\)
\(\Rightarrow-a\cdot b=-\left(a\cdot b\right)=-32\)
4/ \(-2\left(3x+2\right)=1^2+2^2+3^2\)
\(\Leftrightarrow-6x-4=1+4+9\)
\(\Leftrightarrow-6x=14+4\)
\(\Leftrightarrow-6x=18\)
\(\Leftrightarrow x=\frac{18}{-6}\)
\(\Rightarrow x=3\)
TB
1
20 tháng 2 2022
a: =>-12<x<2y<-9
=>x=-11; y=-5
b: =>-7<3(x-1)<8
\(\Leftrightarrow3\left(x-1\right)\in\left\{-6;-3;0;3;6\right\}\)
\(\Leftrightarrow x-1\in\left\{2;1;0;-1;-2\right\}\)
hay \(x\in\left\{3;2;1;0;-1\right\}\)
LM
0
NT
0
M
2
1 tháng 2 2022
Lớp 4?
a) \(\dfrac{x+1}{4}=\dfrac{36}{x+1}\)
\(\Rightarrow\left(x+1\right)^2=144\)
\(\Rightarrow\left[{}\begin{matrix}x+1=12\\x+1=-12\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=11\\x=-13\end{matrix}\right.\)
Vậy: \(x\in\left\{11;-13\right\}\)
b) \(\dfrac{x}{7}=\dfrac{55x-4}{28}\)
\(\Rightarrow4x=55x-4\)
\(\Rightarrow-51x=-4\)
\(\Rightarrow x=\dfrac{4}{51}\)
Vậy: \(x=\dfrac{4}{51}\)
BT
1 tháng 2 2022
a) \(\dfrac{x + 1}{4} = \dfrac{36}{x + 1} \)
\(\Rightarrow\) \(( x + 1 )( x + 1 ) = 36 . 4 \)
\(\Rightarrow ( x + 1 )^2 = 144 \)
\(\Rightarrow ( x + 1 )^2 = 12^2 = ( -12 )^2 \)
\(\Rightarrow\) \(x + 1 ∈ \) { \(12 ; -12 \) }
\(\Rightarrow \) \(x \) \(∈ \) { \(11 ; -13 \) }
Vậy \(x ∈ \) { \(11 ; -13 \) }
NT
1
NC
18 tháng 8 2020
Bài làm:
Ta có: \(a^2.\left(a+1\right)=36\)
\(\Leftrightarrow a^3+a^2-36=0\)
\(\Leftrightarrow\left(a^3-3a^2\right)+\left(4a^2-12a\right)+\left(12a-36\right)=0\)
\(\Leftrightarrow a^2\left(a-3\right)+4a\left(a-3\right)+12\left(a-3\right)=0\)
\(\Leftrightarrow\left(a-3\right)\left(a^2+4a+12\right)=0\)
Mà \(a^2+4a+12=\left(a+2\right)^2+8>0\)
\(\Rightarrow a-3=0\Rightarrow a=3\)
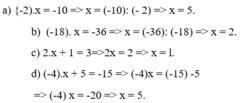
Ta có :
\(\frac{x+1}{2}=\frac{36}{x}\)
\(\Leftrightarrow\)\(x\left(x+1\right)=2.36\)
\(\Leftrightarrow\)\(x\left(x+1\right)=72\)
\(\Leftrightarrow\)\(x\left(x+1\right)=8.9\)
\(\Leftrightarrow\)\(x=8\) ( vì x và (x+1) là hai nguyên liên tiếp )
Vậy \(x=8\)
\(\frac{x+1}{2}\)= \(\frac{36}{x}\)
=> ( x + 1 ) . x = 36 . 2
=> ( x + 1 ) . x = 72 ( 1 )
mà x + 1 ; x là hai số tự nhiên liên tiếp ( 2 )
Từ 1 và 2 => x thuộc { - 8 ; 8 }
Vậy x thuộc { - 8 ; 8 }