tim số tn x bt 5x . 5x + 1 . 5x + 2 = 10.....0 ( 18 c/s 0 ) : 218
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
14 tháng 7 2023
a: =>2^4x<2^28
=>4x<28
=>x<7
b: =>5^3x+3<5
=>3x+3<1
=>3x<-2
=>x<-2/3
9 tháng 8 2021
Bạn thử xem lại đề nhé, giữa 3 số này là dấu cộng hay dấu nhân.
Nếu là dấu cộng thì ta có:
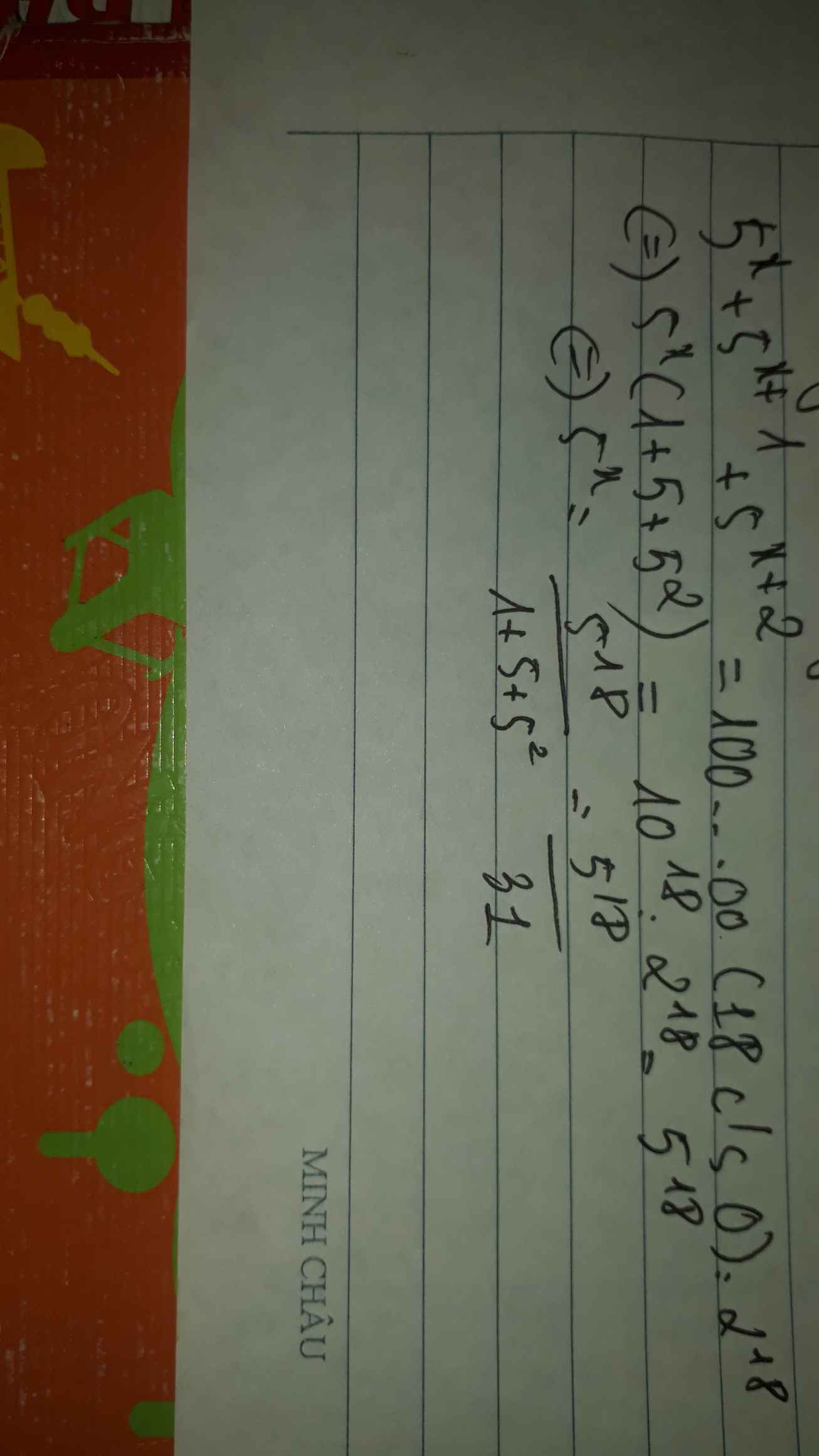
Nếu là dấu nhân thì ta có:
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 3 2019
Mặt cầu (S) có tâm \(I\left(1;0;0\right)\) bán kính \(R=1\)
Do mặt phẳng (P) song song với (Q)
\(\Rightarrow\) Phương trình (P) có dạng: \(5x-12z+a=0\)
Do (P) tiếp xúc với (S) \(\Rightarrow d\left(I;\left(P\right)\right)=R\)
\(\Rightarrow\frac{\left|5.1+0.0-12.0+a\right|}{\sqrt{5^2+0^2+\left(-12\right)^2}}=1\Leftrightarrow\left|a+5\right|=13\Rightarrow\left[{}\begin{matrix}a=8\\a=-18\end{matrix}\right.\)
\(\Rightarrow\) Có hai pt (P) thỏa mãn: \(\left[{}\begin{matrix}5x-12z+8=0\\5x-12z-18=0\end{matrix}\right.\)
Đáp án A
T
11 tháng 6 2019
Phân tích đa thức thành nhân tử:(em làm luôn đấy,ko ghi lại đề)
\(\left(x^3+y^3\right)-\left(x+y\right)+3xy\left(x+y\right)\)
\(=\left(x+y\right)\left(x^2-xy+y^2\right)-\left(x+y\right)+3xy\left(x+y\right)\)
\(=\left(x+y\right)\left(x^2+2xy+y^2-1\right)\)\(=\left(x+y\right)\left[\left(x+y\right)^2-1^2\right]\)
\(=\left(x+y\right)\left(x+y-1\right)\left(x+y+1\right)\)
DT
11 tháng 6 2019
\(8x^3+12x^2+6x+1=0.\)
\(\Leftrightarrow\left(2x\right)^3+3.\left(2x\right)^2.1+3.2x.1^2+1^3=0\)
\(\Leftrightarrow\left(2x+1\right)^3=0\)
\(\Leftrightarrow2x+1=0\)
\(\Leftrightarrow x=-\frac{1}{2}\)
\(2x^2+5x-3=0\Leftrightarrow\left(2x^2+6x\right)+\left(-x-3\right)=0\)
\(\Leftrightarrow2x\left(x+3\right)-\left(x+3\right)=0\Leftrightarrow\left(x+3\right)\left(2x-1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}2x-1=0\\x+3=0\end{cases}\Leftrightarrow}\orbr{\begin{cases}x=\frac{1}{2}\\x=-3\end{cases}}\)
\(x^2-2x-3=0\Leftrightarrow\left(x^2-3x\right)+\left(x-3\right)=0\)
\(\Leftrightarrow x\left(x-3\right)+\left(x-3\right)=0\Leftrightarrow\left(x+1\right)\left(x-3\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x+1=0\\x-3=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=-1\\x=3\end{cases}.}\)
\(\left(5x-1\right)+2\left(1-5x\right)\left(4+5x\right)+\left(5x+4\right)^2\)
\(=5x-1+2\left(4+5x-20x-25x^2\right)+25x^2+40x+16\)
\(=25x^2+45x+15+8+10x-40x-50x^2\)
\(=-25x^2+15x+23\)
\(\left(x-y\right)^3+\left(y+x\right)^3+\left(y-x\right)^3-3xy\left(x+y\right)\)
\(=\left(x-y\right)^3-\left(x-y\right)^3+\left(x+y\right)^3-3x^2y-3xy^2\)
\(=\left(x+y\right)^3-3x^2y-3xy^2\)
\(=x^3+3x^2y+3xy^2+y^3-3xy^2-3x^2y\)
\(=x^3+y^3\)
JS
15 tháng 2 2020
20) -5-(x + 3) = 2 - 5x ⇔ -5 - x - 3 = 2 -5x ⇔ 4x = 10 ⇔ x = \(\frac{5}{2}\)
Vậy...
1 tháng 8 2017
\(\left(x-4\right)\left(x-5\right)\left(x-8\right)\left(x-10\right)=72x^2\)
\(\Leftrightarrow\left(x-4\right)\left(x-5\right)\left(x-8\right)\left(x-10\right)-72x^2=0\)
\(\Leftrightarrow\left(x^2-14x+40\right)\left(x^2-13x+40\right)-72x^2=0\)
\(\Leftrightarrow\left(x^2-13,5x+40-0,5x\right)\left(x^2-13,5x+40+0,5x\right)-72x^2=0\)
\(\Leftrightarrow\left(x^2-13,5x+40\right)^2-\left(0,5x\right)^2-72x^2=0\)
\(\Leftrightarrow\left(x^2-13,5x+40\right)^2-72,25x^2=0\)
\(\Leftrightarrow\left(x^2-13,5x+40+8,5x\right)\left(x^2-13,5x+40-8,5x\right)=0\)
\(\Leftrightarrow\left(x^2-5x+40\right)\left(x^2-22x+40\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2-5x+40=0\left(VN\right)\\x^2-22x+40=0\Leftrightarrow\left[{}\begin{matrix}x=20\\x=2\end{matrix}\right.\end{matrix}\right.\)
1 tháng 8 2017
Câu a,c xem lại đề, cách làm giống câu b, còn câu e giống câu d
b) \(2x^4+5x^3+x^2+5x+2=0\)
Ta nhận thấy x=0 không phải là 1 nghiệm của phương trình, chia cả 2 vế của phương trình cho \(x^2\ne0\), ta được:
\(2x^2+5x+1+\dfrac{5}{x}+\dfrac{2}{x^2}=0\)
\(\Leftrightarrow2\left(x^2+\dfrac{1}{x^2}\right)+5\left(x+\dfrac{1}{x}\right)+1=0\)
Đặt \(y=x+\dfrac{1}{x}\Rightarrow x^2+\dfrac{1}{x^2}=y^2-2\)
\(\Leftrightarrow2\left(y^2-2\right)+5y+1=0\)
\(\Leftrightarrow2y^2+5y-3=0\)
PT đơn giản, tự giải nha, ta được nghiệm y=1/2 và y=-3
Với y=1/2 thì không tìm được x
Với y=-3 thì tìm được 2 nghiệm, tự giải
LN
1
11 tháng 10 2021
\(3x+4=0\Leftrightarrow x=-\dfrac{4}{3}\\ 2x\left(x-1\right)-\left(1+2x\right)=-34\\ \Leftrightarrow2x^2-2x-1-2x=-34\\ \Leftrightarrow2x^2-4x+33=0\\ \Leftrightarrow2\left(x^2-2x+1\right)+30=0\\ \Leftrightarrow2\left(x-1\right)^2+30=0\\ \Leftrightarrow x\in\varnothing\left[2\left(x-1\right)^2+30\ge30>0\right]\\ x^2+9x-10=0\\ \Leftrightarrow x^2-x+10x-10=0\\ \Leftrightarrow\left(x-1\right)\left(x+10\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=1\\x=-10\end{matrix}\right.\\ \left(7x-1\right)\left(2+5x\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}7x-1=0\\2+5x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{7}\\x=-\dfrac{2}{5}\end{matrix}\right.\)
\(5^x.5^{x+1}.5^{x+2}=10....0:2^{18}\Rightarrow100..0:2^{18}=5^{18}.2^{18}:2^{18}=5^{18}\)
\(5^x.5^{x+1}.5^{x+2}\Rightarrow x+x+1+x+2=5^{18}\)
\(\Rightarrow3x+3=18\)
\(\Rightarrow3x=15\)
\(\Rightarrow x=5\)
Vậy x = 5