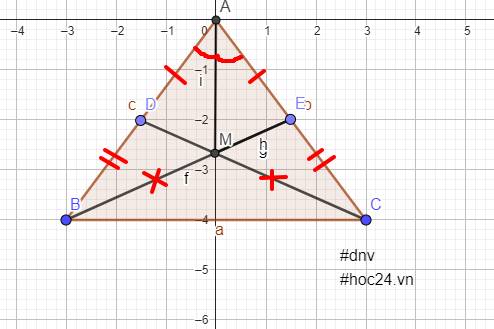
Cho tam giác ABC cân tại A, trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho AD = AE. Gọi M là giao điểm của BE và CD. Chứng minh rằng :
a) BE=CD
b)tam giác BMD = tam giác CME
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a.Xét tam giác DBC và tam giác ECB có:
DB=EC (AB=AC và AD=AE)
góc ABC = góc ACB (cân tại A)
BC là cạnh chung
Do đó tam giác DBC = tam giác ECB (c.g.c)
Suy ra BE= CD (ĐPCM)

a: Xét ΔAEBvà ΔADC có
AE=AD
góc A chung
AB=AC
=>ΔAEB=ΔADC
=>BE=CD
b: Xét ΔMDB và ΔMEC có
góc MDB=góc MEC
DB=EC
góc MBD=góc MCE
=>ΔMDB=ΔMEC
c: Xét ΔAMB và ΔAMC có
MA chung
MB=MC
AB=AC
=>ΔAMB=ΔAMC
=>góc BAM=góc CAM
=>AM là phân giác của góc BAC
`@`` \text {dnv}`
`a,`
Xét `\Delta ABE` và `\Delta ACD`:
`\text {AB = AC (Tam giác ABC cân tại A)}`
`\hat {A}`` \text {chung}`
`\text {AD = AE (gt)}`
`=> \Delta ABE = \Delta ACD (c-g-c)`
`-> \text {BE = CD (2 cạnh tương ứng)}`
`b,`
Vì `\Delta ABE = \Delta ACD (a)`
$ -> \widehat {ACD} = \widehat {ABE} (\text {2 góc tương ứng})$
`->` $\widehat {ADC} = \widehat {AEB} (\text {2 góc tương ứng})$
Ta có: \(\left\{{}\begin{matrix}\widehat{ADC}+\widehat{BDC}=180^0\\\widehat{AEB}+\widehat{CEB}=180^0\end{matrix}\right.\)
$\widehat {ADC} = \widehat {AEB}$
`->` $\widehat {CEB} = \widehat {BDC}$
Ta có:\(\left\{{}\begin{matrix}\text{AB = AD + DB}\\\text{AC = AE + EC}\end{matrix}\right.\)
Mà: \(\left\{{}\begin{matrix}\text{AB = AC}\\\text{AD = AE}\end{matrix}\right.\)
`-> \text {BD = EC}`
Xét `\Delta BMD` và `\Delta CME`:
\(\widehat{\text{DBM}}=\widehat{\text{ECM}}\left(\text{CMT}\right)\)
\(\text{BD = CE (CMT)}\)
\(\widehat{\text{BDM}}=\widehat{\text{CEM}\text{ }}\text{ }\left(\text{CMT}\right)\)
`=> \Delta BMD = \Delta CME (g-c-g)`
`c,` Đề có phải là "Chứng minh AM là phân giác của góc BAC" ?
Vì `\Delta BMD = \Delta CME (b)`
`-> \text {MB = MC (2 cạnh tương ứng)}`
Xét `\Delta BAM` và `\Delta CAM`:
`\text {AB = AC} (\Delta ABC \text {cân tại A})`
`\text {AM chung}`
`\text {MB = MC (CMT)}`
`=> \Delta BAM = \Delta CAM (c-c-c)`
`->` $\widehat {BAM} = \widehat {CAM} (\text {2 góc tương ứng})$
`-> `\(\text{AM là tia phân giác của }\widehat{\text{BAC}}\)

a: Kẻ DH và EK lần lượt vuông góc với BC
=>DH//EK
H,B lần lượt là hình chiếu của D,B trên BC
=>HB là hình chiếu của DB trên BC
K,C lần lượt là hình chiếu của E,C trên BC
=>KC là hình chiếu của EC trên BC
Xét ΔDHB vuông tại H và ΔEKC vuông tại K có
DB=EC
góc DBH=góc ECK
=>ΔDHB=ΔEKC
=>BH=KC và DH=EK
b: Xét ΔABE và ΔACD có
AB=AC
góc BAE chung
AE=AD
=>ΔABE=ΔACD
=>BE=CD
c: Xét ΔMDB và ΔMEC có
góc MDB=góc MEC
DB=EC
góc MBD=góc MCE
=>ΔMDB=ΔMEC
d: Xét ΔABM và ΔACM có
AM chung
MB=MC
AB=AC
=>ΔABM=ΔACM
=>góc BAM=góc CAM
=>AM là phân giác của góc BAC

Bài giải
* Hình tự vẽ
a) Xét tam giác AEB và tam giác ADC có:
Góc A là góc chung
AD = AE (gt)
AB = AC ( tam giác ABC cân tại A )
-> Tam giác AEB = tam giác ADC (c-g-c)
-> BE = CD (hai cạnh tương ứng)
a) Tam giác ABC cân tại A nên AB = AC .
Xét hai tam giác ABE và ACD có: AB = AC, góc A chung và AE = AD nên tam giác ABE = tam giác ACD.
=> BE = CD
P/s: b) , c) bn tự lm nhé, xin lỗi!