Cho hai đường tròn (O), (O') cắt nhau tại A, B. Một đường thẳng cắt hai đường tròn trên tại 4 điểm C, D, E, K theo thứ tự trên đường thẳng ấy. a) Chứng minh góc DBE = góc C + góc K. b) Chứng minh góc CAK + góc DBE = 180 độ
Mn giup e vs a thanks
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KN
20 tháng 3 2020
P/S: Hình như đề bị nhầm, phải là \(\widehat{CAK}+\widehat{DBE}=180^0\)chứ
Vẽ dây chung AB của hai đường tròn (O) và (Q)
Xét (Q) có \(\widehat{CAB}=\widehat{DEB}\)(hai góc nội tiếp cùng chắn cung BC)
Xét (O) có \(\widehat{BAK}=\widehat{BDE}\)(hai góc nội tiếp cùng chắn cung BF)
\(\Delta BDE\)có \(\widehat{BEB}+\widehat{BDE}+\widehat{DBE}=180^0\)
Do đó \(\widehat{CAK}+\widehat{DBE}=\widehat{CAB}+\widehat{BAK}+\widehat{DBE}=\widehat{DEB}+\widehat{BDE}+\widehat{DBE}=180^0\)
Vậy \(\widehat{CAK}+\widehat{DBE}=180^0\)(đpcm)
20 tháng 3 2020
sửa giùm mình dòng 3 sau cái hình là cung BK chứ ko pk BF, nhầm
12 tháng 6 2018
a) Xét tứ giác ABOC: ^ABO=^ACO=900 (Do AB và AC là 2 tiếp tuyến của (O))
=> Tứ giác ABOC nội tiếp đường tròn dường kính AO (1)
Ta có: DE là dây cung của (O), I là trung điểm DE => OI vuông góc DE => ^OIA=900
Xét tứ giác ABOI: ^ABO=^OIA=900 => Tứ giác ABOI nội tiếp đường tròn đường kính AO (2)
(1) + (2) => Ngũ giác ABOIC nội tiếp đường tròn
Hay 4 điểm B;O;I;C cùng thuộc 1 đường tròn (đpcm).
b) Gọi P là chân đường vuông góc từ D kẻ đến OB
Ta có: Tứ giác BOIC nội tiếp đường tròn => ^ICB=^IOP (Góc ngoài tại đỉnh đối) (3)
Dễ thấy tứ giác DIPO nội tiếp đường tròn đường kính OD
=> ^IOP=^IDP (=^IDK) (4)
(3) + (4) => ^ICB=^IDK (đpcm).
c) ^ICB=^IDK (cmt) => ^ICH=^IDH => Tứ giác DHIC nội tiếp đường tròn
=> ^DIH=^DCH hay ^DIH=^DCB.
Lại có: ^DCB=^DEB (2 góc nội tiếp cùng chắn cung BD) => ^DIH=^DEB
Mà 2 góc trên đồng vị => IH // EB hay IH // EK
Xét tam giác KDE: I là trung điểm DE (Dễ c/m); IH // EK; H thuộc DK
=> H là trung điểm DK (đpcm).
CM
11 tháng 4 2019
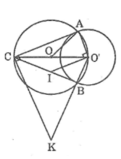
Trong đường tròn (O’) ta có AC và BC là hai tiếp tuyến cắt nhau tại C
Suy ra: 
(tính chất hai tiếp tuyến cắt nhau)
Mà O’I ⊥ O’A (gt)
CA ⊥ O’A (chứng minh trên)
Suy ra: O’I // CA => 
(hai góc so le trong)
Suy ra: 
Hay tam giác CIO’ cân tại I => IC = IO’
Khi đó I nằm trên đường trung trực của O’C
Lại có: 
(tính chất hai tiếp tuyến cắt nhau)
KC ⊥ CA (gt)
O’A ⊥ AC (chứng minh trên)
Suy ra: KC // O’A => 
(hai góc so le trong)
Suy ra: 
Hay tam giác CKO’ cân tại K => KC = KO’
Khi đó K nằm trên đường trung trực của O’C
Mặt khác: OC = OO’ (= R)
Suy ra O, I, K nằm trên đường trung trực của O’C
Vậy O, I, K thẳng hàng.
CM
8 tháng 9 2018
a, HS tự chứng minh
b, Chứng minh ∆NMC:∆NDA và ∆NME:∆NHA
c, Chứng minh ∆ANB có E là trực tâm => AE ⊥ BN mà có AK ⊥ BN nên có ĐPCM
Chứng minh tứ giác EKBH nội tiếp, từ đó có A K F ^ = A B M ^
d, Lấy P và G lần lượt là trung điểm của AC và OP
Chứng minh I thuộc đường tròn (G, GA)