Từ một điểm P nằm ngoài (O) ,kẻ cát tuyến PAB.Gọi D là điểm chính giữa cung AB.Kẻ đường kính DE,PE cắt (O) tại I, ID cắt AB tại K.Chứng minh rằng PA.KB=PB KA
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
28 tháng 4 2021
1) Ta có: N là điểm chính giữa của cung AB(gt)
nên ON\(\perp\)AB tại I
hay MN\(\perp\)AB tại I
Xét (O) có
\(\widehat{NEM}\) là góc nội tiếp chắn nửa đường tròn
nên \(\widehat{NEM}=90^0\)(Hệ quả góc nội tiếp)
hay \(\widehat{FEM}=90^0\)
Xét tứ giác MIFE có
\(\widehat{MIF}\) và \(\widehat{FEM}\) là hai góc đối
\(\widehat{MIF}+\widehat{FEM}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: MIFE là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
CM
16 tháng 10 2018
a, M C D ^ = B I D ^ = 1 2 s đ C D ⏜
b, Sử dụng kết quả câu a)
CH
Cô Hoàng Huyền
Admin
VIP
30 tháng 1 2018
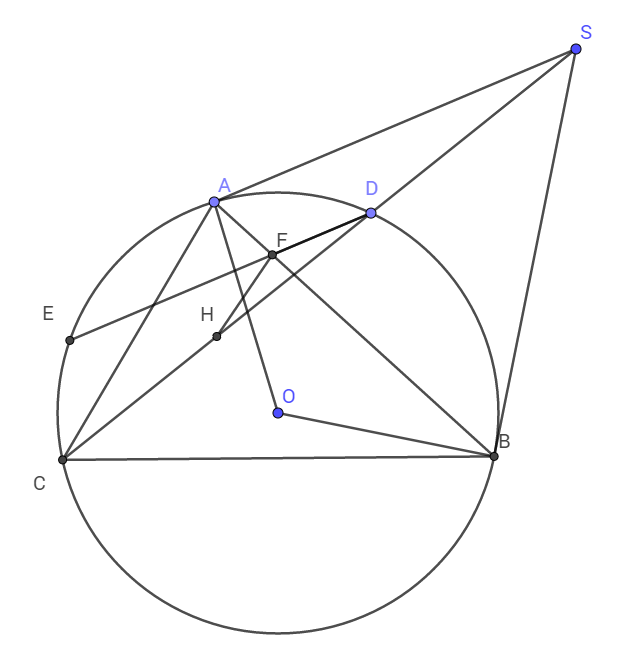
Ta có các tam giác vuông AOS; HOS, BOS có chung cạnh huyền OS nên S, A, H, O, B nội tiếp đường tròn đường kính OS.
Khi đó ta có :
\(\widehat{ASH}=\widehat{ABH}\) (Hai góc nội tiếp cùng chắn cung AH)
Mà \(\widehat{ASH}=\widehat{FDH}\) (Hai góc đồng vị)
\(\Rightarrow\widehat{ABH}=\widehat{FDH}\)
Suy ra tứ giác HFDO nội tiếp.
Từ đó ta có \(\widehat{FHD}=\widehat{ABD}\)(Hai góc nội tiếp)
Mà \(\widehat{ABD}=\widehat{ACD}\) (Hai góc nội tiếp)
Nên \(\widehat{FHD}=\widehat{ACD}\)
Chúng lại ở vị trí đồng vị nên HF // AC.