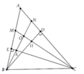
Cho tam giác ABC. Các tia phân giác của góc B và C cắt nhau tại O, lần lượt cắt AC và AB tại M và N. Cho biết BN+CM=BC
1) CMR tam giác MON là tam giác cân
2) Tính số đo các góc của tam giác MON
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu hỏi của Nguyễn Quang Nam - Toán lớp 8 - Học toán với OnlineMath
Tham khảo bài 3 tại link trên nhé!

Xét ΔABC có M,N lần lượt là trung điểm của AB,AC
=>MN là đường trung bình của ΔABC
=>MN//BC và \(MN=\dfrac{1}{2}BC\)
Xét ΔOMN và ΔOCB có
\(\widehat{OMN}=\widehat{OCB}\)(hai góc so le trong, NM//BC)
\(\widehat{MON}=\widehat{COB}\)(hai góc đối đỉnh)
Do đó: ΔOMN~ΔOCB
=>\(\dfrac{MN}{CB}=\dfrac{ON}{OB}=\dfrac{1}{2}\)
Ta có \(AN=\dfrac{1}{2}AC\)
=>\(S_{ABN}=\dfrac{1}{2}\cdot S_{ABC}=66\left(m^2\right)\)
Ta có: M là trung điểm của AB
=>\(S_{BMN}=\dfrac{1}{2}\cdot S_{BNA}=\dfrac{1}{2}\cdot66=33\left(cm^2\right)\)
\(\dfrac{ON}{OB}=\dfrac{1}{2}\)
=>\(\dfrac{OB}{ON}=2\)
=>\(\dfrac{OB+ON}{ON}=2+1=3\)
=>\(\dfrac{BN}{ON}=3\)
=>\(\dfrac{ON}{BN}=\dfrac{1}{3}\)
=>\(S_{MON}=\dfrac{1}{2}\cdot S_{MNB}=\dfrac{1}{2}\cdot33=16,5\left(cm^2\right)\)

a) Sử dụng tính chất tổng các góc trong một tam giác bằng 1800.
⇒ A B C ^ = A E C ^ ⇒ N B D ^ = M C A ^
Trong DDBN có: N B D ^ + B N D ^ = 90 0
Gọi O = CM Ç BN Þ CM ^ BN = O (1)
b) Xét DCNK có: CO ^ KN Þ CO ^ BN, CO là phân giác A C E ^ nên DCNK cân ở C Þ O là trung điểm KN (2).
Tương tự chứng minh được là trung điểm MH (3).
Từ (1),(2) và (3) suy ra MNHK là hình thoi.