Cho tam giác ABC vuông tại A . Gọi M là điểm tùy ý thuộc cạnh BC . I và K là hình chiếu của M trên các cạnh AB và AC . Trên tia đối của tia IM lấy D sao cho ID = IM . Trên tia đối của tia KM lấy E sao cho KE = KM
a) C/m : tam giác ADM cân
b) C/m : tam giác CME cân
c) C/m : D , A , E thẳng hàng
d) C/m : BD // CE
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔAMD có
AI vừa là đường cao, vừa là trung tuyến
=>ΔAMD cân tại A
=>AB là phân giác của góc MAD(1) và AM=AD
Xét ΔAME có
AC vừa là đường cao, vừa là trung tuyến
=>ΔAME cân tại A
=>AC là phân giác của góc MAE(2); AM=AE
=>AE=AD
b: Từ (1), (2) suy ra góc DAE=2*90=180 độ
=>D,A,E thẳng hàng

(a) \(I,M\) là trung điểm của \(AB,BC\Rightarrow IM\) là đường trung bình của \(\Delta ABC\Rightarrow\left\{{}\begin{matrix}IM\left|\right|AC\Leftrightarrow MD\left|\right|AC\left(1\right)\\IM=\dfrac{1}{2}AC\end{matrix}\right.\)
Lại có: \(IM=ID\Rightarrow MD=2IM=2\cdot\dfrac{1}{2}AC=AC\left(2\right)\)
Từ \(\left(1\right),\left(2\right)\Rightarrow ADMC\) là hình bình hành (điều phải chứng minh).
(b) \(\left\{{}\begin{matrix}MI\left|\right|AC\left(cmt\right)\\AC\perp AB\left(gt\right)\end{matrix}\right.\Rightarrow MI\perp AB\Rightarrow\hat{AIM}=90^o\left(3\right)\).
\(M,K\) là trung điểm của \(BC,AC\Rightarrow MK\) là đường trung bình của \(\Delta ABC\Rightarrow MK\left|\right|AB\), mà \(AB\perp AC\left(gt\right)\Rightarrow MK\perp AC\Rightarrow\hat{AKM}=90^o\left(4\right)\).
Ta cũng có: \(\hat{A}=90^o\left(5\right)\).
Từ \(\left(3\right),\left(4\right),\left(5\right)\Rightarrow AIMK\) là hình chữ nhật (điều phải chứng minh).
(c) Do \(AIMK\) là hình chữ nhật (chứng minh trên) nên \(\left\{{}\begin{matrix}AK\left|\right|MI\Leftrightarrow AK\left|\right|ID\\AK=MI=ID\end{matrix}\right.\Rightarrow AKID\) là hình bình hành \(\Rightarrow IK\left|\right|AD\left(6\right)\).
Lại có: \(I,K\) là trung điểm của \(MD,MQ\Rightarrow IK\) là đường trung bình của \(\Delta MQD\Rightarrow IK\left|\right|QD\left(7\right)\)
Từ \(\left(6\right),\left(7\right)\Rightarrow Q,A,D\) thẳng hàng (điều phải chứng minh).

a) Xét ΔIMC vuông tại I và ΔINC vuông tại I có
CI chung
MI=NI(gt)
Do đó: ΔIMC=ΔINC(hai cạnh góc vuông)
b) Ta có: ΔIMC=ΔINC(cmt)
nên (hai góc tương ứng)
hay
Xét ΔBAC vuông tại A và ΔKAC vuông tại A có
AC chung
(cmt)
Do đó: ΔBAC=ΔKAC(cạnh góc vuông-góc nhọn kề)
⇒CB=CK(hai cạnh tương ứng)
Ta có: MI⊥AC(gt)
AB⊥AC(ΔABC vuông tại A)
Do đó: MI//AB(Định lí 1 từ vuông góc tới song song)
hay MN//KB
Xét ΔCKB có
M là trung điểm của CB(gt)
MN//KB(cmt)
Do đó: N là trung điểm của CK(Định lí 1 đường trung bình của tam giác)
c) Ta có: MA=ME(gt)
mà A,M,E thẳng hàng
nên M là trung điểm của AE
Xét tứ giác ABEC có
M là trung điểm của đường chéo BC(gt)
M là trung điểm của đường chéo AE(cmt)
Do đó: ABEC là hình bình hành(Dấu hiệu nhận biết hình bình hành)
hay AB//EC(Hai cạnh đối trong hình bình hành ABEC)
d) Ta có: ABEC là hình bình hành(cmt)
nên AB=EC(Hai cạnh đối trong hình bình hành ABEC)
mà AB=AK(ΔCBA=ΔCKA)
nên EC=AK
Ta có: AB//EC(Cmt)
nên CE//KA
Xét tứ giác AECK có
CE//AK(cmt)
CE=AK(cmt)
Do đó: AECK là hình bình hành(Dấu hiệu nhận biết hình bình hành)
Xét ΔCAB có
M là trung điểm của BC(gt)
MI//AB(cmt)
Do đó: I là trung điểm của AC(Định lí 1 đường trung bình của tam giác)
Ta có: AECK là hình bình hành(cmt)
nên Hai đường chéo AC và EK cắt nhau tại trung điểm của mỗi đường(Định lí hình bình hành)
mà I là trung điểm của AC(cmt)
nên I là trung điểm của EK
hay E,I,K thẳng hàng(đpcm)
chúc bạn học tốt nha cái này mình cũng không chắc là đúng đó bạn :)
a) Xét ΔIMC vuông tại I và ΔINC vuông tại I có
CI chung
MI=NI(gt)
Do đó: ΔIMC=ΔINC(hai cạnh góc vuông)
b) Ta có: ΔIMC=ΔINC(cmt)
nên \(\widehat{MCI}=\widehat{NCI}\)(hai góc tương ứng)
hay \(\widehat{BCA}=\widehat{KCA}\)
Xét ΔCAB vuông tại A và ΔCAK vuông tại A có
CA chung
\(\widehat{BCA}=\widehat{KCA}\)(cmt)
Do đó: ΔCAB=ΔCAK(Cạnh góc vuông-góc nhọn kề)
Suy ra: CA=CK(hai cạnh tương ứng)
Ta có: CN+NK=CK(N nằm giữa C và K)
CM+MB=CB(M nằm giữa C và B)
mà CK=CB(cmt)
và CN=CM(ΔCNI=ΔCMI)
nên NK=MB
mà \(MB=\dfrac{BC}{2}\)(M là trung điểm của BC)
nên \(NK=\dfrac{BC}{2}\)
mà BC=KC(cmt)
nên \(NK=\dfrac{CK}{2}\)
mà điểm N nằm giữa hai điểm C và K
nên N là trung điểm của CK(đpcm)
c) Xét ΔAMB và ΔEMC có
MA=ME(gt)
\(\widehat{AMB}=\widehat{EMC}\)(hai góc đối đỉnh)
MB=MC(M là trung điểm của BC)
Do đó: ΔAMB=ΔEMC(c-g-c)
Suy ra: \(\widehat{MAB}=\widehat{MEC}\)(hai góc tương ứng)
mà \(\widehat{MAB}\) và \(\widehat{MEC}\) là hai góc ở vị trí so le trong
nên AB//EC(Dấu hiệu nhận biết hai đường thẳng song song)

a: Xét ΔIMC vuông tại I và ΔINC vuông tại I có
CI chung
IM=IN
Do đó: ΔIMC=ΔINC

a) Xét ΔIMC vuông tại I và ΔINC vuông tại I có
CI chung
MI=NI(gt)
Do đó: ΔIMC=ΔINC(hai cạnh góc vuông)
b) Ta có: ΔIMC=ΔINC(cmt)
nên \(\widehat{MCI}=\widehat{NCI}\)(hai góc tương ứng)
hay \(\widehat{BCA}=\widehat{KCA}\)
Xét ΔBAC vuông tại A và ΔKAC vuông tại A có
AC chung
\(\widehat{BCA}=\widehat{KCA}\)(cmt)
Do đó: ΔBAC=ΔKAC(cạnh góc vuông-góc nhọn kề)
⇒CB=CK(hai cạnh tương ứng)
Ta có: MI⊥AC(gt)
AB⊥AC(ΔABC vuông tại A)
Do đó: MI//AB(Định lí 1 từ vuông góc tới song song)
hay MN//KB
Xét ΔCKB có
M là trung điểm của CB(gt)
MN//KB(cmt)
Do đó: N là trung điểm của CK(Định lí 1 đường trung bình của tam giác)
c) Ta có: MA=ME(gt)
mà A,M,E thẳng hàng
nên M là trung điểm của AE
Xét tứ giác ABEC có
M là trung điểm của đường chéo BC(gt)
M là trung điểm của đường chéo AE(cmt)
Do đó: ABEC là hình bình hành(Dấu hiệu nhận biết hình bình hành)
hay AB//EC(Hai cạnh đối trong hình bình hành ABEC)
d) Ta có: ABEC là hình bình hành(cmt)
nên AB=EC(Hai cạnh đối trong hình bình hành ABEC)
mà AB=AK(ΔCBA=ΔCKA)
nên EC=AK
Ta có: AB//EC(Cmt)
nên CE//KA
Xét tứ giác AECK có
CE//AK(cmt)
CE=AK(cmt)
Do đó: AECK là hình bình hành(Dấu hiệu nhận biết hình bình hành)
Xét ΔCAB có
M là trung điểm của BC(gt)
MI//AB(cmt)
Do đó: I là trung điểm của AC(Định lí 1 đường trung bình của tam giác)
Ta có: AECK là hình bình hành(cmt)
nên Hai đường chéo AC và EK cắt nhau tại trung điểm của mỗi đường(Định lí hình bình hành)
mà I là trung điểm của AC(cmt)
nên I là trung điểm của EK
hay E,I,K thẳng hàng(đpcm)
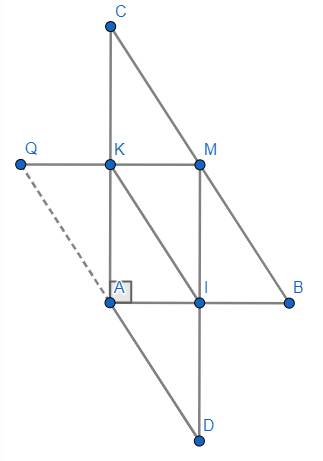


a) vì I và E là hình chiếu => góc MIA= góc MKA=90 đô.Rui cm tam giác DIA =tam giác MIA(c-g-c).
b)tam giác MKC= tam giác CKE(c-g-c)
c)tam giác DIA=tam giác MIA> góc DAI= góc MAI=> góc DAI+MAK=90 độ( vì góc IAM+góc MAK=90 độ) tương tự Cm góc EAK+ óc MAI=90 độ Nên góc DAI+IAM+MAK+KAE= 180 độ<=> DAE thẳng hàng
d)CM BD//AM rùi CM AM//CE<=> BD//CE