Cho tam giác A'B'C' đồng dạng tam giác ABC theo tỉ số k=\(\frac{1}{3}\). Biết AB=7, AC=10, BC = 9. Tính A'B', A'C', B'C'
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
13 tháng 9 2023
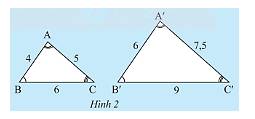
a) Từ kí hiệu của hình vẽ ta thấy các cặp góc bằng nhau là:
\(\widehat A = \widehat {A'};\widehat B = \widehat {B'};\widehat C = \widehat {C'}\)
b) Ta có:
\(\frac{{A'B'}}{{AB}} = \frac{6}{4} = \frac{3}{2};\frac{{A'C'}}{{AC}} = \frac{{7,5}}{5} = \frac{3}{2};\frac{{B'C'}}{{BC}} = \frac{9}{6} = \frac{3}{2}\).
Ta thấy, \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = \frac{3}{2}\)
13 tháng 9 2023
a: góc A=góc A'; góc B=góc B'; góc C=góc C'
b: A'B'/AB=A'C'/AC=B'C'/BC
KT
29 tháng 4 2018
a) Ta có: \(\frac{4}{8}=\frac{5}{10}=\frac{6}{12}\left(=\frac{1}{2}\right)\)
hay \(\frac{AB}{A'B'}=\frac{AC}{A'C'}=\frac{BC}{B'C'}\)
\(\Rightarrow\)\(\Delta A'B'C'~\Delta ABC\)
b) \(\Delta A'B'C'~\Delta ABC\)
\(\Rightarrow\)\(\frac{P_{A'B'C'}}{P_{ABC}}=\frac{A'B'}{AB}=\frac{8}{4}=2\)
22 tháng 1 2019
Xin chào các bạn !!!
Hãy Đăng Kí Cho Channel Kaito1412_TV Để nhé !
Link là : https://www.youtube.com/channel/UCqgS-egZEJIX-ON873XpD_Q/videos?view_as=subscriber
19 tháng 3 2020
vì tam giác ABC đồng dạng với tam giác A'B'C' =>AB/A'B'=BC/B'C'=AC/A'C'
=>BC/B'C'=6/8=3/4=>BC=3.10/4=15/2(cm)
ta lại có AC/A'C'=3/4
=>A'C'/4=AC/3=3/1=3
=>AC=9cm=>A'C'=12(cm)
Vậy BC=15/2 cm ,AC=9cm,A'C'=12cm