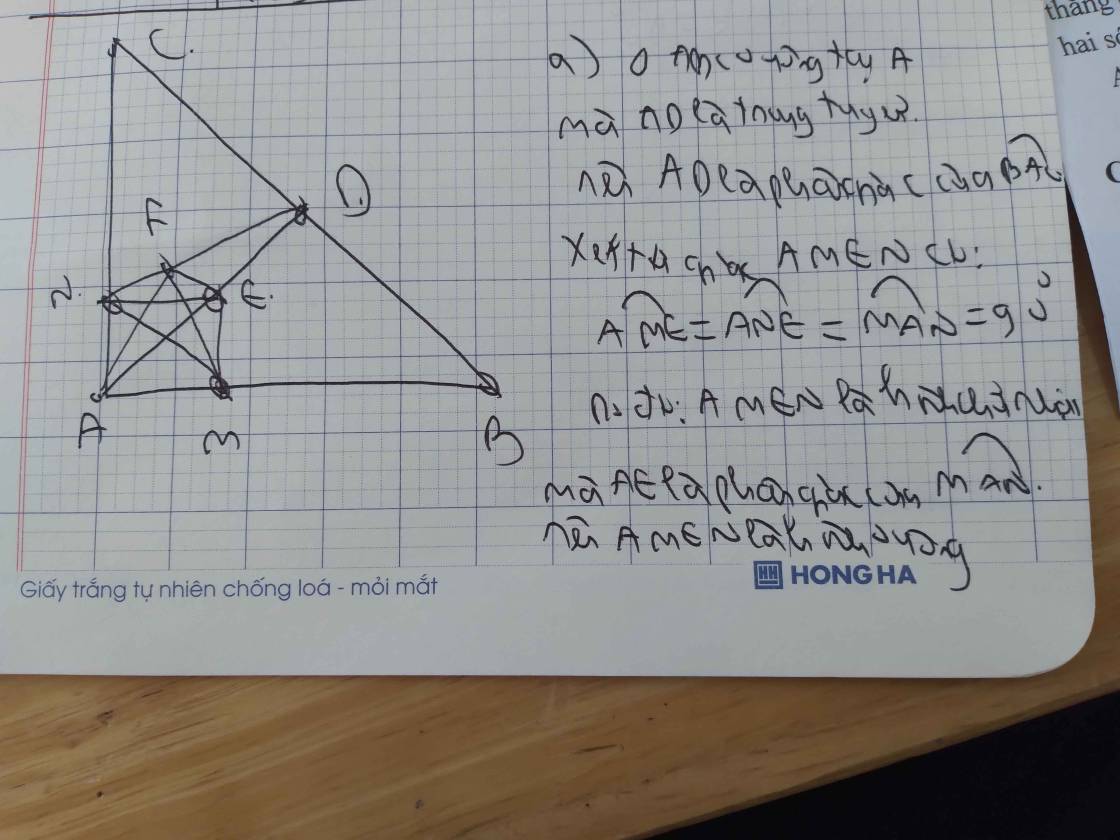
cho tam giác ABC vuông cân tại A.Gọi M là trung điểm của BC.Vẽ điểm D bất kì nằm giũa M và C .Kẻ dường thẳng qua D vuông góc với AD tại A
a, Chứng Minh: AM vuông BC
b,Chứng minh: tam giác ABH=ACK
c,chứng minh: tam giác AHM=CKM
d, chứng minh: tam gác MAK là tam giác vuông cân


Tham khảo bài này nha bạn:
Cho tam giác ABC vuông cân tại A. M là trung điểm của BC.điểm E nằm giữa M và C. kẻ BH, CK vuông góc?
với AE (H,K thuộc AE ).
a. cm: BH=AK
b, tam giác MBH= tam giác MAK
c, tam giác MHK vuông cân.
a) Ta có ^ABH + ^BAH = 90° Măt khác ^CAH + ^BAH = 90°
=> ^ABH = ^CAH
Xét ▲ABH và ▲CAK có:
^H = ^C (= 90°)
AB = AC (T.g ABC vuông cân)
^ABH = ^CAH (cmt)
=> △ABH = △CAK (c.h-g.n)
=> BH = AK
b) Ta có BH//CK (Cùng ┴ AK)
=>^HBM = ^MCK (SLT)(1)
Mặt khác ^MAE + ^AEM = 90°(2)
Và ^MCK + ^CEK = 90°(3)
Nhưng ^AEM = ^CEK (đ đ)(4)
Từ 2,3,4 => ^MAE = ^ECK (5)
Từ 1,5 => ^HBM = ^MAE
Ta lại có AM là trung tuyến của tam giác vuông ABC nên AM = BM =MC = 1/2 BC
Xét ▲MBH và ▲MAK có:
MB = AM (cmt); ^HBM = ^MAK(cmt); BH = AK (cma)
=> △MBH = △MAK (c.g.c)
c) Theo câu a, b ta có: AH = CK; MH = MK; AM = MC nên : ▲AMH = ▲ CMK (c.c.c)
=> ^AMH = ^CMK; mà ^AMH + ^HMC = 90 độ
=> ^CMK + ^HMC = 90° hay ^HMK = 90°
Tam giác HMK có MK = MH và ^HMK = 90° nên vuông cân