Cho hình chữ nhật có chiều dài 4cm, chiều rộng 3cm. Trên các cạnh của hình chữ nhật này lấy 14 điểm sao cho khoảng cách giữa hai điểm liên tiếp đều là 1 cm (hình vẽ). Có bao nhiêu tam giác với các đỉnh là 3 trong số 14 điểm đó mà diện tích bằng 6cm2?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Vẽ hình chữ nhật ABCD có chiều dài 5cm, chiều rộng 4cm .
Nối trung điểm M của AD với trung điểm N của cạnh BC ta được các hình tứ giác đều là hình chữ nhật.
b) – Các hình chữ nhật có trong hình bên là:
Hình chữ nhật ABCD, ABNM, MNCD.
- Các cạnh song song với cạnh AB là:
Các cạnh MN và DC.

Tham khảo:
a)
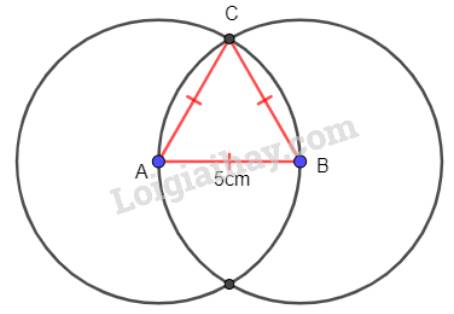
- Kẻ đoạn thẳng AB=5cm.
- Dùng compa vẽ 2 đường tròn bán kính 5cm có tâm lần lượt là A và B.
- Điểm C là giao điểm của hai đường tròn đó.
ABC là tam giác đều cần vẽ.
b)
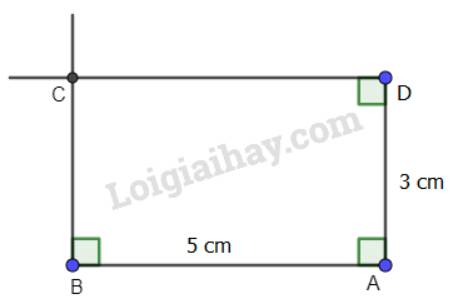
- Vẽ đoạn thẳng AB=5cm và đoạn thẳng AD=3cm vuông góc với nhau.
- Qua B kẻ đường thẳng vuông góc với AB.
- Qua D kẻ đường thẳng vuông góc với AD.
- Hai đường thẳng này cắt nhau ở C.
ABCD là hình chữ nhật cần vẽ.
c)
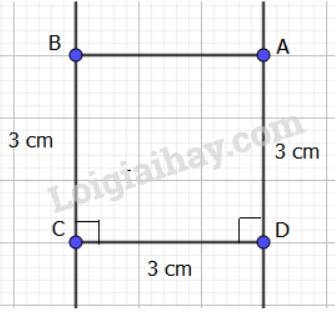
- Vẽ đoạn thẳng CD dài 3cm.
- Vẽ hai đường thẳng vuông góc với CD tại C và D như hình vẽ.
- Trên đường thẳng qua C lấy đoạn thẳng CB=3cm; trên đường thẳng qua D lấy đoạn thẳng DA=3cm.
- Nối 2 điểm A và B ta được hình vuông cần vẽ.
d)
- Vẽ đoạn thẳng AB=6cm.
- Vẽ đường tròn tâm A bán kính 8cm.
- Qua A kẻ đường thẳng vuông góc với AB. Trên đường thẳng lấy H sao cho AH=4cm.
- Qua H kẻ đường thẳng vuông góc với AH cắt đường tròn tại điểm D (chọn 1 trong 2 giao điểm).
- Qua B kẻ đường thẳng song song với AD.
- Qua D kẻ đường thẳng song song với AB.
- Hai đường thẳng cắt nhau tại C.
ABCD là hình bình hành cần vẽ.
e)
- Vẽ đoạn thẳng AB = 5cm.
- Vẽ đường tròn tâm A bán kính 5 cm. Trên đường tròn này lấy điểm D.
- Từ D vẽ đường thẳng song song với AB. Trên đường thẳng này lấy điểm C sao cho DC = 5 cm.
- Nối C với B ta được hình thoi ABCD có cạnh 5 cm.
Ta được ABCD là hình thoi cần vẽ.

Học sinh vẽ hình chữ nhật ABCD
Trên cạnh AD lấy điểm M sao cho: AM = 4 : 2 = 2 (cm)
Trên cạnh BC lấy điểm N sao cho: BN = 2cm
M và N là trung điểm của AD và BC
- Các hình chữ nhật có ở hình bên là: ABNM, MNCD, ABCD
- Các cạnh song song với cạnh AB là: MN, DC

a) Học sinh vẽ hình chữ nhật ABCD
b) Trên cạnh AD lấy điểm M sao cho: AM = 4 : 2 = 2 (cm)
Trên cạnh BC lấy điểm N sao cho: BN = 2cm
M và N là trung điểm của AD và BC
- Các hình chữ nhật có ở hình bên là: ABNM, MNCD, ABCD
- Các cạnh song song với cạnh AB là: MN, DC

Khoảng cách lớn nhất giữa 2 cây liên tiếp =45m, khi đó tổng số cây = 6
* * *
* * *

Gọi khoảng cách lớn nhất giữa hai cây liên tiếp là a.
Ta có : \(84⋮a\)
\(20⋮a\)\(\Rightarrow a\inƯC\left(84,20\right)\)
Mà \(84=2^2.3.7\) \(20=2^2.5\)
\(\RightarrowƯCLN\left(84,20\right)=2^2=4\)
\(\Rightarrow a=4\)
Chu vi khu vườn là :
\(\left(84+20\right)x2=208\) \(\left(m\right)\)
Tổng số cây khi đó là :
\(208:4=52\) ( cây )

a) Chiều dài của hình chữ nhật là:
3 : ( 5 - 4 ) x 5 = 15 (cm)
Chiều rộng của hình chữ nhật là:
15 - 3 = 12 (cm)
Diện tích của hình chữ nhật là:
15 x 12 = 180 (cm2)
Đáp số:180 cm2
b) Ta có hình vẽ:
SDBE=\(\frac{1}{3}\)SDCB= 12 x 3 = 36 (cm2) vì :
+Có chung chiều cao hạ từ D xuống BC
+Đáy BE=\(\frac{1}{3}\)đáy BC
SADC là : 180 - 36 = 144 (cm2)
Đường cao CD là :144 x 2 : 8 = 36 (cm)
Cạnh AB dài là : 180 x 2 : 36 = 10 (cm)
Đáp Số : a)180cm2
b)10 cm

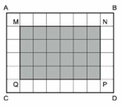
Chia miếng bìa ABCD thành các ô vuông, mỗi ô vuông có cạnh là 5 cm. Số ô vuông của miếng bìa đó là : 8 x 6 = 48 (ô vuông). Số ô vuông của hình chữ nhật MNPQ là : 6 x 4 = 24 (ô vuông) Vì 48 : 24 = 2 (lần) nên hình chữ nhật MNPQ có diện tích đúng bằng diện tích hình cắt đi. Mặt khác các cạnh của hình chữ nhật MNPQ song song và cách đều các cạnh tương ứng của miếng bìa ABCD. Vì vậy hình MNPQ đúng là hình chữ nhật bị cắt đi. Mỗi cặp cạnh tương ứng của hình ABCD và MNPQ cách nhau 5 cm.
Chia miếng bìa ABCD thành các ô vuông, mỗi ô vuông có cạnh là 5 cm. Số ô vuông của miếng bìa đó là : 8 x 6 = 48 (ô vuông). Số ô vuông của hình chữ nhật MNPQ là : 6 x 4 = 24 (ô vuông) Vì 48 : 24 = 2 (lần) nên hình chữ nhật MNPQ có diện tích đúng bằng diện tích hình cắt đi. Mặt khác các cạnh của hình chữ nhật MNPQ song song và cách đều các cạnh tương ứng của miếng bìa ABCD. Vì vậy hình MNPQ đúng là hình chữ nhật bị cắt đi. Mỗi cặp cạnh tương ứng của hình ABCD và MNPQ cách nhau 5 cm.

Chia miếng bìa ABCD thành các ô vuông, mỗi ô vuông có cạnh là 5 cm. Số ô vuông của miếng bìa đó là : 8 x 6 = 48 (ô vuông).
Số ô vuông của hình chữ nhật MNPQ là : 6 x 4 = 24 (ô vuông)
Vì 48 : 24 = 2 (lần) nên hình chữ nhật MNPQ có diện tích đúng bằng diện tích hình cắt đi. Mặt khác các cạnh của hình chữ nhật MNPQ song song và cách đều các cạnh tương ứng của miếng bìa ABCD. Vì vậy hình MNPQ đúng là hình chữ nhật bị cắt đi. Mỗi cặp cạnh tương ứng của hình ABCD và MNPQ cách nhau 5 cm.
Xét hai trường hợp:
Trường hợp 1: Không có hai đỉnh nào của tam giác cùng nằm trên một cạnh hình chữ nhật (hình vẽ dưới đây)
Kí hiệu các khoảng cách từ L, M, A tới đường thẳng CI lần lượt là \(h_L,h_M,h_A\) thì \(h_M\le h_L\) hoặc \(h_L\le h_A\). Suy ra
\(dt_{MCI}< dt_{LCI}< dt_{ALH}=6cm^2\)hoặc \(dt_{MCI}< dt_{ACI}< dt_{AEI}=6cm^2\).
2) Trường hợp tam giác có hai đỉnh nằm trên cùng một cạnh của hình chữ nhật (hình vẽ sau)
Trường hợp này, dễ thấy tam giác có diện tích 6cm2 khi và chỉ khi tam giác có 2 đỉnh trùng với hai đỉnh hình chữ nhật và đỉnh còn lại nằm trên cạnh đối diện. Số tam giác với đáy LH là 5. Số tam giác với đáy AE là 5. Số tam giác với đáy AL là 4; Số tam giác với đáy EH là 4. Vậy số tam giác thỏa mãn yêu cầu đề bài là 14.
14 nhé bạn