Các công thức số chỉnh hợp, tổ hợp, hoán vị?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


- Cho tập hợp X gồm n phần tử phân biệt (n ≥ 0). Mỗi cách sắp xếp n phần tử của X theo một thứ tự nào đó được gọi là một hoán vị của n phần tử. Số các hoán vị của n phần tử được ký hiệu là Pn. Công thức : Pn = n! = 1.2…n. Quy ước: 0! = 1.
- Chỉnh hợp (không lặp) chập k () của n phần tử đó là một bộ sắp thứ tự k phần tử của A, các phần tử đôi một khác nhau.Công thức : A(n,k)=(n!)/((n-k)!)
- Tổ hợp chập k các phần tử của A (0<=k<=n)là một tâp con k phần tử (0<=k<=n) của tập A. Công thức : C(n,k)=(n!)/(k!(n-k)!)
(( **** và kết bạn với mình nhé :) )

Đáp án C
Công thức tính số chỉnh hợp chập k của n: A n k = n ! n − k ! .
Công thức tính số tổ hợp chập k của n : C n k = n ! k ! n − k ! .
Hai tính chất cơ bản của tổ hợp: C n k = C n n − k
C n + 1 k = C n k + C n k − 1
Quan sát các đáp án đã cho ta thấy đáp án C đúng.

Đáp án: D.
Hướng dẫn: D
Xét cặp gen Ab//aB giảm phân xảy ra hoán vị với tần số 18% tạo ra tỉ lệ giao tử là:
A B = - a b - = 18% : 2 = 9%.
Cặp Dd giảm phân cho 2 loại giao tử là D = d = 0,5.
Vậy tỉ lệ giao tử hoán vị gen của tổ hợp gen Ab//aB là:
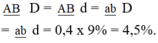

Đáp án C
A b a B , f = 18% → AB = ab = 0,09; Ab = aB = 0,41
Dd → 0,5D : 0,5d
→ABD = abD = ABd = abd = 0,09 x 0,5 = 0,045 = 4,5%



n!=1.2.3...nn!=1.2.3...n. Quy ước: 0!=10!=1
n!=(n−1)!nn!=(n−1)!n
n!p!=(p+1)(p+2)....nn!p!=(p+1)(p+2)....n (với n>pn>p)
n!(n−p)!=(n−p+1)(n−p+2)....nn!(n−p)!=(n−p+1)(n−p+2)....n (với n>pn>p)
2. Hoán vị (không lặp)
Một tập hợp gồm n phần tử (n≥1)(n≥1). Mỗi cách sắp xếp n phần tử này theo một thứ tự nào đó được gọi là một hoán vị của n phần tử.
Số hoán vị của n phần tử là Pn=n!Pn=n!
3. Hoán vị lặp
Cho k phần tử khác nhau a1;a2;...;aka1;a2;...;ak . Mỗi cách sắp xếp n phần tử trong đó gồm n1 phần tử a1; n2 phần tử a2;…; nk phần tử ak (n1+n2+...+nk=n)(n1+n2+...+nk=n) theo một thứ tự nào đó được gọi là một hoán vị lặp cấp n và kiểu (n1;n2;...;nk)(n1;n2;...;nk) của k phần tử
Số các hoán vị lặp cấp n kiểu (n1;n2;;;;nk)(n1;n2;;;;nk) của k phần tử là:
Pn(n1;n2;...;nk)=n!n1!n2!...nk!Pn(n1;n2;...;nk)=n!n1!n2!...nk!

HƯỚNG DẪN GIẢI