Chứng minh rằng trong mọi ngũ giác lồi ta luôn tìm được ba đường chéo , từ đó có thể lập được một tam giác
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

xét hình ngũ giác ta thấy có tất cả là 5 đường chéo mà theo như đề bài đã cho thì mỗi đường chéo cắt ra khỏi một tam giác có diện tích bằng 1.
=> có tất cả 5 hình tam giác được cắt ra.
diện tích hình ngũ giác:
S=S1+S2+S3+S4+S5=1+1+1+1+1=5
( S1...5là tam giác 1.....tam giác 5 0

HD: Chọn ra 3 đỉnh bất kỳ của đa giác có: C 10 3 cách chọn.
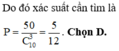
■ Số tam giác có 2 cạnh là cạnh của đa giác là: 10
(vì ứng với mỗi đỉnh ta lấy 2 cạnh kề với nó là được tgiác như điều kiện đã xét)
■ Số tam giác có 1 cạnh là cạnh của đa giác là: 10.6 = 60 vì chọn 1 cạnh của đa giác, ta chọn được 6 đỉnh để tạo tam giác (trừ đi 2 đỉnh của cạnh đó và 2 đỉnh nằm kề sát cạnh đó), mà có 10 cạnh như thế nên có 10.6 = 60
Suy ra số tgiác được tạo thành từ các đường chéo của đa giác là: 120 - 10 - 60 = 50 tam giác.
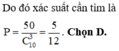
chỉ cần vẽ hình ra rồi nối và kết luận