- Xét mặt cắt quả bóng là một hình tròn. Điểm C chia đường kính AB thành hai đoạn AC : CB = 3 : 4. Biết rằng diện tích hình tròn là 35 cm2. Tuổi của tôi là số đo diện tích hình được tô màu cam. Các bạn hãy tính xem năm nay Quang Hải bao nhiêu tuổi?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Để tính diện tích bông hoa, ta cần biết diện tích của một nửa hình tròn.
Gọi cạnh hình vuông là a. Diện tích hình vuông ABCD là a^2 = 400 cm^2.
Vậy a = √400 = 20 cm.
Đường kính của nửa hình tròn là cạnh hình vuông, nên đường kính của nửa hình tròn là 20 cm.
Bán kính của nửa hình tròn là đường kính chia 2, nên bán kính của nửa hình tròn là 20/2 = 10 cm.
Diện tích của một nửa hình tròn là (1/2)πr^2, với r là bán kính.
Diện tích của một nửa hình tròn là (1/2)π(10 cm)^2 = 50π cm^2.
Vì bông hoa có 4 cánh, nên diện tích bông hoa là 4 lần diện tích của một nửa hình tròn.
Diện tích bông hoa là 4 x 50π cm^2 = 200π cm^2.
Kết quả cuối cùng là diện tích bông hoa là 200π cm^2.

Xin lỗi mình cũng có câu hỏi y như bạn
thông cảm nha!

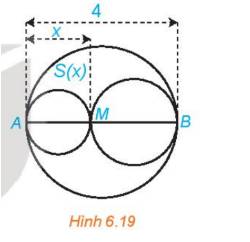
Ta có: AM<AB nên \(0 < x < 4\)
Diện tích hình tròn đường kính AB là \({S_0} = \pi .{\left( {\frac{{AB}}{2}} \right)^2} = 4\pi \)
Diện tích hình tròn đường kính AM là \({S_1} = \pi .{\left( {\frac{{AM}}{2}} \right)^2} = \frac{{\pi .{x^2}}}{4}\)
Diện tích hình tròn đường kính MB là \({S_2} = \pi .{\left( {\frac{{MB}}{2}} \right)^2} = \pi .\frac{{{{\left( {4 - x} \right)}^2}}}{4}\)
Diện tích phần hình phẳng nằm trong hình tròn lớn và nằm ngoài hai hình tròn nhỏ là \(S(x) = {S_0} - {S_1} - {S_2} = 4\pi - \frac{{{x^2}}}{4}\pi - \frac{{{{\left( {4 - x} \right)}^2}}}{4}\pi = \frac{{ - {x^2} + 4x}}{2}\pi \)
Vì diện tich S(x) không vượt quá 1 nửa tổng diện tích hai hình tròn nhỏ nên:
\(S(x) \le \frac{1}{2}\left( {{S_1} + {S_2}} \right)\)
Khi đó : \(\frac{{ - {x^2} + 4x}}{2}\pi \le \frac{1}{2}.\frac{{{x^2} - 4x + 8}}{2}\pi \)
\( \Leftrightarrow - {x^2} + 4x \le \frac{{{x^2} - 4x + 8}}{2}\)
\( \Leftrightarrow - 2{x^2} + 8x \le {x^2} - 4x + 8\)
\( \Leftrightarrow 3{x^2} - 12x + 8 \ge 0\)
Xét tam thức \(3{x^2} - 12x + 8\) có \(\Delta ' = 12 > 0\) nên f(x) có 2 nghiệm phân biệt \({x_1} = \frac{{6 - 2\sqrt 3 }}{3};{x_2} = \frac{{6 + 2\sqrt 3 }}{3}\)
Mặt khác a=3>0, do đó ta có bảng xét dấu:
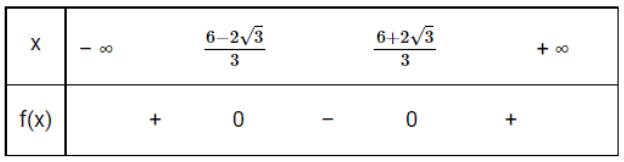
Do đó \(f(x) \ge 0\) với mọi \(x \in \left( { - \infty ;\frac{{6 - 2\sqrt 3 }}{3}} \right] \cup \left[ {\frac{{6 + 2\sqrt 3 }}{3}; + \infty } \right)\)
Mà 0<x<4 nên \(x \in \left( { - \infty ;\frac{{6 - 2\sqrt 3 }}{3}} \right] \cup \left[ {\frac{{6 + 2\sqrt 3 }}{3}; + \infty } \right)\)