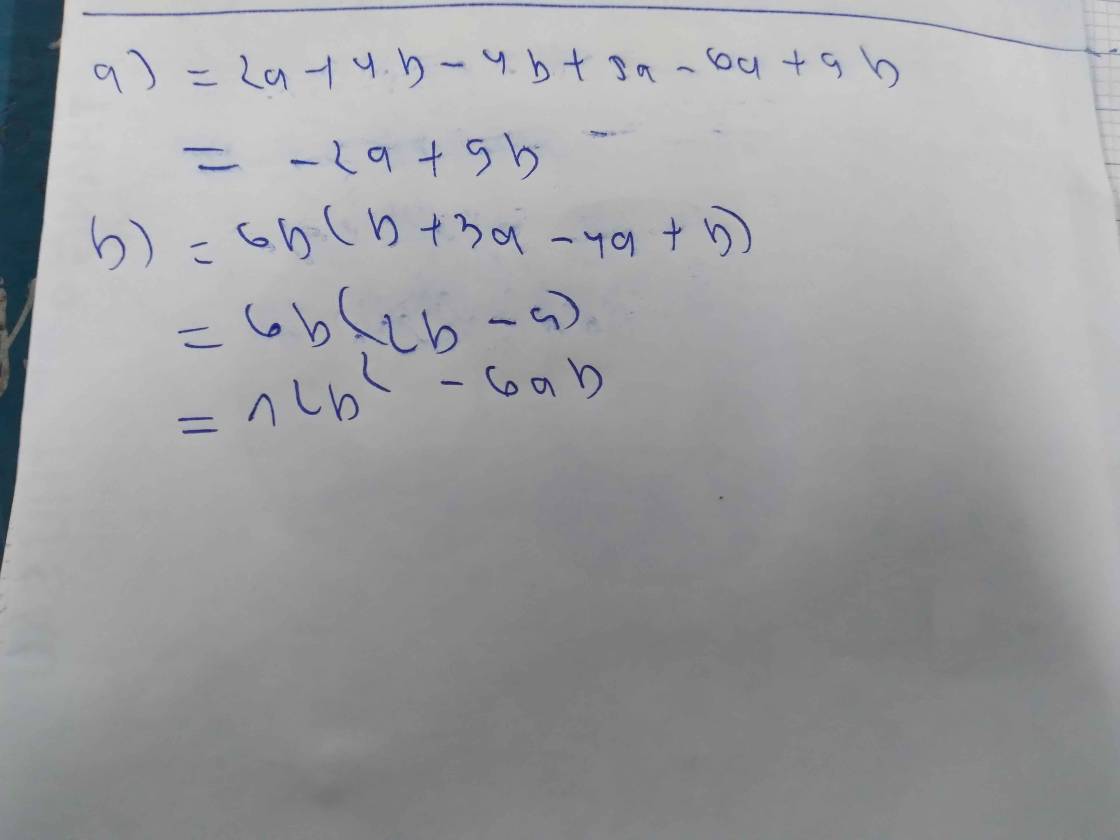Cho \(a^2+b^2+9=6a+4b\) Tìm Min, Max của \(Q=3a +4b\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VA
0
DT
0
ND
1
AH
Akai Haruma
Giáo viên
7 tháng 3 2020
Lời giải:
Áp dụng BĐT Cô-si cho các số không âm:
$a^2+1\geq 2\sqrt{a^2}=2|a|\geq 2a$
$b^2+16\geq 2\sqrt{16b^2}=2|4b|\geq 8b$
$\Rightarrow a^2+b^2+17\geq 2(a+4b)=2.17$
$\Rightarrow a^2+b^2\geq 17$
Vậy $A_{\min}=17$ khi $a=1; b=4$
Với từng ấy điều kiện đề bài thì không tìm được max của $a^2+b^2$
MP
11 tháng 9 2023
\(a.2a+4b+\left(-4b+5a\right)-\left(6a-9b\right)\)
\(=2a+4b-4b+5a-6a+9b\)
\(=\left(2a+5a-6a\right)+\left(4b-4b+9b\right)\)
\(=a+9b\)
\(b.6a\left[b+3a-\left(4a-b\right)\right]\)
\(=6a\left[b+3a-4a+b\right]\)
\(=6a\left[4a-a+b+b\right]\)
\(=6a\left(3a-2b\right)\)
23 tháng 11 2016
\(\frac{a}{b}=\frac{4}{7}\Rightarrow\frac{a}{4}=\frac{b}{7}=k\)
=> a = 4k ; b = 7k
Thay vào đẳng thức ta có :
4b2 - 6a2 = 49
4.(7k)2 - 6.(4k)2 = 49
4.49.k2 - 6.16.k2 = 49
k2(4.49 - 6.16) = 49
k2 . 100 = 49
=> \(k^2=\frac{49}{100}\)
=> \(k=\left[\begin{array}{nghiempt}\frac{7}{10}\\-\frac{7}{10}\end{array}\right.\)
Với k = 7/10
=> \(a=\frac{4.7}{10}=\frac{28}{10}=2,8\)
\(b=\frac{7.7}{10}=\frac{49}{10}=4,9\)
=> 3a + 2b = 3. 2,8 + 2. 4,9 = 8,4 + 9,8 = 18,2
Với k = -7/10
\(\Rightarrow a=\frac{4.\left(-7\right)}{10}=-\frac{28}{10}=-2,8\)
\(b=\frac{7.\left(-7\right)}{10}=-\frac{49}{10}=-4,9\)
=> 3a + 2b = 3 . (-2,8) + 7 . (-4,9) = (-8,4) + (-9,8) = -18,2
=> Trị nhỏ nhất là -18,2
ND
1
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 3 2020
\(\left(4a-b\right)^2=\left(2\sqrt{2}.\sqrt{2}a-\frac{1}{2}.2b\right)^2\le\left(8+\frac{1}{4}\right)\left(2a^2+4b^2\right)=1089\)
\(\Rightarrow-33\le4a-b\le33\)
\(\Rightarrow-67\le M\le-1\)
\(M_{min}\) khi \(\left\{{}\begin{matrix}a=-8\\b=1\end{matrix}\right.\)
\(M_{max}\) khi \(\left\{{}\begin{matrix}a=8\\b=-1\end{matrix}\right.\)