12+12+32x=24
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NK
1
18 tháng 9 2021
Đk \(x\ge\dfrac{3}{2}\)
\(\Leftrightarrow3\sqrt{2x-3}-4\sqrt{2x-3}=1-2\sqrt{2x-3}\)
\(\Leftrightarrow\sqrt{2x-3}=1\)
\(\Leftrightarrow2x-3=1\)
\(\Leftrightarrow x=2\)
Vậy S=\(\left\{2\right\}\)
NH
3
2
13 tháng 8 2023
`\sqrt{8x-4}-2\sqrt{18x-9}+2\sqrt{32x-16}=12` `ĐK: x >= 1/2`
`<=>2\sqrt{2x-1}-6\sqrt{2x-1}+8\sqrt{2x-1}=12`
`<=>4\sqrt{2x-1}=12`
`<=>\sqrt{2x-1}=3`
`<=>2x-1=9`
`<=>x=5` (t/m)
Vậy `S={5}`.
13 tháng 8 2023
\(\Leftrightarrow2\sqrt{2x-1}-2\cdot3\sqrt{2x-1}+2\cdot4\sqrt{2x-1}=12\)
=>\(4\sqrt{2x-1}=12\)
=>\(\sqrt{2x-1}=3\)
=>2x-1=9
=>2x=10
=>x=5
2 tháng 10 2018
\(27x^3-27x^2+18x-4\)
\(=27x^3-9x^2-18x^2+6x+12x-4\)
\(=9x\left(3x-1\right)-6x\left(3x-1\right)+4\left(3x-1\right)\)
\(=\left(3x-1\right)\left(9x^2-6x+4\right)\)
\(x^2+2xy+y^2-x-y-12\)
\(=\left(x+y\right)^2-\left(x+y\right)-12\)
\(=\left(x+y\right)^2-4\left(x+y\right)+3\left(x+y\right)-12\)
\(=\left(x+y\right)\left(x+y-4\right)+3\left(x+y-4\right)=\left(x+y+3\right)\left(x+y-4\right)\) \(P=\left(x+2\right)\left(x+3\right)\left(x+4\right)\left(x+5\right)-24\)
\(=\left(x^2+7x+10\right)\left(x^2+7x+12\right)-24\) (nhóm 2 cái đầu với cuối lại với nhau, 2 cái giữa vào 1 nhóm)
Đặt \(x^2+7x+11=a\)
Ta có: \(P=\left(a-1\right)\left(a+1\right)-24\)
\(=a^2-25=\left(a-5\right)\left(a+5\right)\)
\(=\left(x^2+7x+6\right)\left(x^2+7x+16\right)=\left(x+1\right)\left(x+6\right)\left(x^2+7x+16\right)\)
d, \(4x^4-32x^2+1\)
\(=4x^4+4x^2+1-36x^2\)
\(=\left(2x+1\right)^2-\left(6x\right)^2=\left(2x^2-6x+1\right)\left(2x^2+6x+1\right)\)
19 tháng 7 2021
Ta có: \(\sqrt{4.5x}+\sqrt{50x}-\sqrt{32x}+\sqrt{72x}-5\sqrt{\dfrac{x}{2}}-12=0\)
\(\Leftrightarrow\dfrac{3\sqrt{2}}{2}\sqrt{x}+5\sqrt{2}\sqrt{x}-4\sqrt{2}\sqrt{x}+6\sqrt{2}\sqrt{x}-\dfrac{5\sqrt{2}}{2}\sqrt{x}-12=0\)
\(\Leftrightarrow6\sqrt{2x}=12\)
\(\Leftrightarrow\sqrt{2x}=2\)
\(\Leftrightarrow2x=4\)
hay x=2
CM
28 tháng 2 2018
Đáp án B
P T 9 x + 9 x 3 = 2 2 .2 x + 2 .2 x ⇔ 4 9 9 x = 3 2 .2 x ⇔ 9 2 x = 9 2 4 ⇔ x = log 9 2 9 2 4 ⇒ a = log 9 2 9 2 4
⇒ P = log 9 2 9 2 4 + 1 2 log 9 2 2 = log 9 2 9 2 4 log 9 2 2 = log 9 2 9 2 = 1
LT
5 tháng 4 2020
1)\(4x^2+32+64\)
\(\Leftrightarrow\left(2x\right)^2+32x+8^2\)
\(\Leftrightarrow\left(2x+8\right)^2\)
2) \(24-3y^2x=3\left(8-y^2x\right)\)
3) \(\left(x-12\right)^2-9\)
\(\Leftrightarrow\left(x-12-9\right)\left(x-12+9\right)\)
\(\Leftrightarrow\left(x-21\right)\left(x-3\right)\)
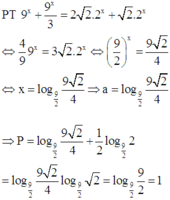
\(12+12+32x=24\)
\(24+32x=24\)
\(32x=24-24\)
\(32x=0\)
\(x=0:32\)
\(x=0\)
12 + 12 + 32x = 24
=> 24 + 32x = 24
=> 32x = 24 - 24
=> 32x = 0
=> x = 0 : 32
=> x = 0
Vậy x = 0