tìm x và y là số nguyên sao cho (2x-1).(y+3)=5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
4 tháng 12 2023
1, để \(\dfrac{2x+1}{x+3}\) là 1 số nguyên
= > 2x + 1 chia hết cho x + 3 ( x thuộc Z và x \(\ne3\) )
= > 2 ( x + 3 ) - 5 chia hết cho x + 3
=> -5 chia hết cho x + 3
hay x + 3 thuộc Ư(-5 ) \(\in\left\{\pm1;\pm5\right\}\)
Đến đây em tự tìm các giá trị của x
2, Tương tự câu 1, x - 1 chia hết cho x + 5 ( x thuộc Z và x khác - 5 )
= > - 6 chia hết cho x + 5
= > \(x+5\in\left\{\pm1;\pm2;\pm3;\pm6\right\}\)
....
3, ( x - 1 ) ( y - 3 ) = 7
x,y thuộc Z = > x - 1 ; y - 3 thuộc Ư(7)
và ( x - 1 )( y - 3 ) = 7
( 1 ) \(\left\{{}\begin{matrix}x-1=1\\y-3=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=10\end{matrix}\right.\)
(2) \(\left\{{}\begin{matrix}x-1=7\\y-3=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=8\\y=4\end{matrix}\right.\)
( 3) \(\left\{{}\begin{matrix}x-1=-1\\y-3=-7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=-4\end{matrix}\right.\)
( 4 ) \(\left\{{}\begin{matrix}x-1=-7\\y-3=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-6\\y=2\end{matrix}\right.\)
Từ ( 1 ) , ( 2 ) , ( 3 ) , ( 4 ) các cặp giá trị ( x,y ) nguyên cần tìm là ....
T
28 tháng 11 2023
Giup mình với ah.
1- Tính :
A= 5. | x- 5 | - 3x + 1
2 - Tìm các số nguyên x,y ; sao cho :
a) 5/x - y/3 = 1/6 b) 5/x + y/4 = 1/8
3- Tìm giá trị lớn nhất của Q = 27-2x/12-x ( x là số nguyên)
---------------------------------------------------------------------------------------------
28 tháng 11 2023
1) \(A=5.\left|x-5\right|-3x+1\)
\(A=\left[{}\begin{matrix}5.\left(x-5\right)-3x+1\left(x-5\ge0\right)\\5.\left(5-x\right)-3x+1\left(x-5< 0\right)\end{matrix}\right.\)
\(A=\left[{}\begin{matrix}5x-25-3x+1\left(x\ge5\right)\\25-5x-3x+1\left(x< 5\right)\end{matrix}\right.\)
\(A=\left[{}\begin{matrix}2x-24\left(x\ge5\right)\\26-8x\left(x< 5\right)\end{matrix}\right.\)
29 tháng 11 2023
3:
\(Q=\dfrac{27-2x}{12-x}=\dfrac{2x-27}{x-12}\)
\(\Leftrightarrow Q=\dfrac{2x-24-3}{x-12}=2-\dfrac{3}{x-12}\)
Để Q lớn nhất thì \(2-\dfrac{3}{x-12}\) lớn nhất
=>\(\dfrac{3}{x-12}\) nhỏ nhất
=>x-12 là số nguyên âm lớn nhất
=>x-12=-1
=>x=11
Vậy: \(Q_{min}=2-\dfrac{3}{11-12}=2+3=5\) khi x=11
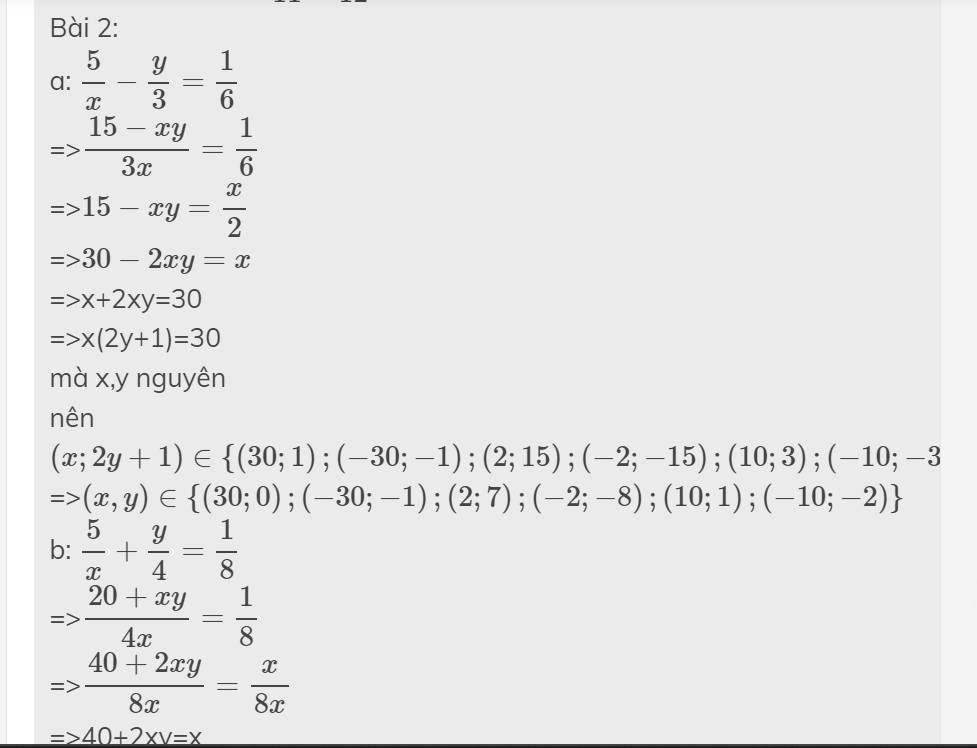
Bài 2:
a: \(\dfrac{5}{x}-\dfrac{y}{3}=\dfrac{1}{6}\)
=>\(\dfrac{15-xy}{3x}=\dfrac{1}{6}\)
=>\(15-xy=\dfrac{x}{2}\)
=>\(30-2xy=x\)
=>x+2xy=30
=>x(2y+1)=30
mà x,y nguyên
nên \(\left(x;2y+1\right)\in\left\{\left(30;1\right);\left(-30;-1\right);\left(2;15\right);\left(-2;-15\right);\left(10;3\right);\left(-10;-3\right)\right\}\)
=>\(\left(x,y\right)\in\left\{\left(30;0\right);\left(-30;-1\right);\left(2;7\right);\left(-2;-8\right);\left(10;1\right);\left(-10;-2\right)\right\}\)
b: \(\dfrac{5}{x}+\dfrac{y}{4}=\dfrac{1}{8}\)
=>\(\dfrac{20+xy}{4x}=\dfrac{1}{8}\)
=>\(\dfrac{40+2xy}{8x}=\dfrac{x}{8x}\)
=>40+2xy=x
=>x-2xy=40
=>x(1-2y)=40
mà x,y nguyên
nên \(\left(x;1-2y\right)\in\left\{\left(40;1\right);\left(-40;-1\right);\left(8;5\right);\left(-8;-5\right)\right\}\)
=>\(\left(x,y\right)\in\left\{\left(40;0\right);\left(-40;1\right);\left(8;-2\right);\left(-8;3\right)\right\}\)
TL
2
21 tháng 6 2016
a) (x+3) . (y+2) =1
<=> (x+3) và (y+2) \(\in\) Ư(1)
=> Ư(1) = {-1;1}
+ Nếu: - x + 3 = 1 <=> x = -2
- y + 2 = 1 <=> x = -1
+Nếu: - x + 3 = -1 <=> x = -4
- y + 2 = -1 <=> x = -3
21 tháng 6 2016
a) (x+3) . ( y+2) = 1
=> (x+3) thuộc Ư(1)
=> ( x+3) thuộc {-1;1}
+) x+3 = -1
=> x = -1-3 = -4
=> y+2 = 1 / -1 = -1 => y = -1-2 = -3
+) x+3 =1
=> x = 1-3 = -2
=> y+2 = 1/1 = 1
=> y = 1-2 = -1
Vậy ta có những cặp (x;y) cần tìm là: (-4;-3) và (-2;-1).
b) (2x-5) . ( y-6) = 17
=> (2x-5) thuộc Ư(17)
=> (2x-5) thuộc {-1;1;-17;17}
Ta có bảng sau:
2x-5 -1 1 -17 17
x 2 3 -6 11
y-6 -17 17 -1 1
y -11 23 5 7
(t/m) (t/m) (t/m) (t/m)
Vậy ta có ccs cặp (x;y) cần tìm là :(2;-11) ; (3;23) ; (-6;5) ; (11;7)
DA
20 tháng 2 2020
a) Vì 2x-1 là bội của x+5 nên 2x-1 \(⋮\)x+5
=> x+5 \(⋮\)x+5
=> ( 2x-1) - ( x+5) \(⋮\)x+5
=> (2x-1) - 2(x+5) \(⋮\)x+5
=> 2x -1 - 2x -10 \(⋮\)x+5
=> -11 \(⋮\)x+5
=> x+5 \(\in\)Ư(11) ={ 1;11; -1; -11}
=> x\(\in\){ -4; 6; -6; -16}
Vậy....
F
1
(2x-1).(y+3)=5
=>(2x-1) và (y+3) thuộc Ư(5) ; x;y thuộc Z
ta có bảng sau :
vậy ta có các cặp x;y thỏa mãn là :
x = 1 ; y = 2
x = 3 ; y = -2
x = 0 ; y = -8
x = -2 ; y = -4