[Toán 7 Cực Khó] Cho tam giác ABC vuông tại A, kẻ AH vuông góc với BC (H thuộc BC); gọi P là giao điểm 3 đường phân giác của tam giác ABH, Q là giao điểm 3 đường phân giác của tam giác AHC. Đường thẳng PQ cắt cạnh AB và AC lần lượt tại E và F. Chứng minh AE=AF
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Sửa đề: Trên HC lấy E sao cho HE=HB và c/m ΔBHA=ΔEHA
Xét ΔBHA vuông tại H và ΔEHA vuông tại H có
AH chung
BH=EH(gt)
Do đó: ΔBHA=ΔEHA(hai cạnh góc vuông)

a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
b: Xét ΔAKH vuông tại K và ΔAFH vuông tại F có
AH chung
\(\widehat{KAH}=\widehat{FAH}\)
Do đó: ΔAKH=ΔAFH
Suy ra: HK=HF
c: Xét ΔABC có AK/AB=AF/AC
nên KF//BC

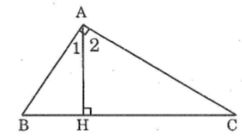
Có thể tìm góc B bằng hai cách:
Cách 1
Ta có: ∠(A1 ) + ∠(A2 ) = ∠(BAC) = 90o(1)
Vì ΔAHB vuông tại H nên:
∠B + ∠(A1) = 90o(tính chất tam giác vuông) (2)
Từ (1) và (2) suy ra ∠B = ∠(A2 )
Cách 2
Vì ΔABC vuông tại A nên:
∠B +∠C = 90o (theo tính chất tam giác vuông) (1)
Vì ΔAHC vuông tại H nên:
∠(A2 ) + ∠C = 90o (tính chất tam giác vuông) (2)
Từ (1) và (2) suy ra: ∠B = ∠(A2)


Có thể tìm góc B bằng hai cách:
Cách 1
Ta có: ∠(A1 ) + ∠(A2 ) = ∠(BAC) = 90o(1)
Vì ΔAHB vuông tại H nên:
∠B + ∠(A1) = 90o(tính chất tam giác vuông) (2)
Từ (1) và (2) suy ra ∠B = ∠(A2 )
Cách 2
Vì ΔABC vuông tại A nên:
∠B +∠C = 90o (theo tính chất tam giác vuông) (1)
Vì ΔAHC vuông tại H nên:
∠(A2 ) + ∠C = 90o (tính chất tam giác vuông) (2)
Từ (1) và (2) suy ra: ∠B = ∠(A2)

a: Xét ΔABC và ΔADE có
AB=AD
\(\widehat{BAC}=\widehat{DAE}\)(hai góc đối đỉnh)
AC=AE
Do đó: ΔABC=ΔADE
b: Xét ΔAHB vuông tại H và ΔAKD vuông tại K có
AB=AD
\(\widehat{ABH}=\widehat{ADK}\)(ΔABC=ΔADE)
Do đó: ΔAHB=ΔAKD
=>BH=DK
c: Ta có: ΔAHB=ΔAKD
=>\(\widehat{HAB}=\widehat{DAK}\)
mà \(\widehat{HAB}+\widehat{HAD}=180^0\)(hai góc kề bù)
nên \(\widehat{DAK}+\widehat{DAH}=180^0\)
=>K,A,H thẳng hàng

Xét ΔDBH vuông tại D và ΔECH vuông tại E có
BH=CH
\(\widehat{B}=\widehat{C}\)
Do đó: ΔDBH=ΔECH
Suy ra: HD=HE
mà HE<HC
nên HD<HC