Trên mặt phẳng tọa độ Oxy tọa độ của điểm M(x;y) phải thỏa mãn điều kiện gì để:
a) M luôn nằm trên trục hoành?
b) M luôn nằm trên trục tung?
c) Điểm M luôn nằm trên đường phân giác của góc vuông phần tư thứ nhất)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

trên mặt phẳng tọa độ Oxy, tọa độ của điểm M(x; y) phải thỏa mãn điều kiện gì để hoành độ bằng 2?
Trả lời:
x=2
mk ko chắc lắm

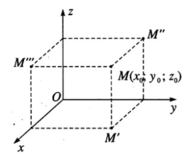
Gọi M’, M’’, M’’’ lần lượt là hình chiếu vuông góc của điểm M trên các mặt phẳng (Oxy), (Oyz), (Ozx).
Ta có:
• M’( x 0 ; y 0 ; 0)
• M’’ (0; y 0 ; z 0 )
• M’’’( x 0 ; 0; z 0 )

\(b,\text{PT hoành độ giao điểm: }-2x+5=x-1\Leftrightarrow x=2\Leftrightarrow y=1\Leftrightarrow A\left(2;1\right)\\ \text{Vậy }A\left(2;1\right)\text{ là giao điểm }\left(d_1\right)\text{ và }\left(d_2\right)\\ c,\text{Gọi }\left(d_3\right):y=ax+b\left(a\ne0\right)\text{ là đt cần tìm}\\ \left(d_3\right)\text{//}\left(d_1\right)\text{ và }M\left(-2;1\right)\in\left(d_3\right)\Leftrightarrow\left\{{}\begin{matrix}a=-2\\b\ne5\\-2a+b=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-2\\b=-1\end{matrix}\right.\\ \Leftrightarrow\left(d_3\right):y=-2x-1\)

Đáp án A.
Tọa độ điểm M 2 ; − 1 ; 1 trên mặt phẳng (Oxy) là M ' 2 ; − 1 ; 0 .

có phương trình hoành độ giao điểm
3/2.x-2=-1/2.x+2<=>3/2.x+1/2.x=2+2
<=>2x=4<=>x=2
thay x=2 vào hàm số y=3/2.x-2=>y=1
vậy đồ thị hàm số y=3/2.x-2 và y=-1/2.x+2 cắt nhau tại điểm M(2;1)

a: 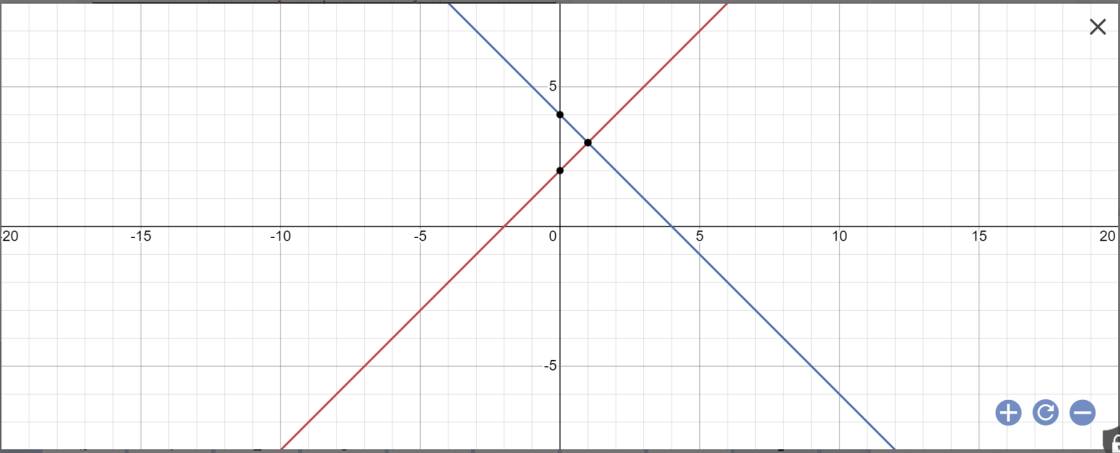
b: Tọa độ giao điểm của (d1) và (d2) là:
\(\left\{{}\begin{matrix}x+2=-x+4\\y=x+2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x=2\\y=x+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=1+2=3\end{matrix}\right.\)
Thay x=1 và y=3 vào (d3), ta được:
\(1\cdot m+m=3\)
=>2m=3
=>\(m=\dfrac{3}{2}\)

\(\text{Đặt }M\left(x;y\right)\\ \overrightarrow{MB}\left(-2-x,2-y\right);\overrightarrow{MC}\left(-x,1-y\right)\\ \left|\overrightarrow{MB}\right|=\left|2\overrightarrow{MC}\right|\Leftrightarrow\sqrt{\left(-2-x\right)^2+\left(2-y\right)^2}=2\sqrt{\left(-x\right)^2+\left(1-y\right)^2}\\ \Leftrightarrow x^2+4x+4+y^2-4y+4=2x^2+2y^2-4y+2\\ \Leftrightarrow x^2+y^2-4y-6=0\\ \text{Mà }M\in Ox\Leftrightarrow y=0\Leftrightarrow x^2-6=0\Leftrightarrow\left[{}\begin{matrix}x=\sqrt{6}\\x=-\sqrt{6}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}M\left(\sqrt{6};0\right)\\M\left(-\sqrt{6};0\right)\end{matrix}\right.\)