Cho đường tròn (O) và điểm A nằm ngoài đường tròn. Vẽ các tiếp tuyến AB và AC với đường tròn (B, C là các tiếp điểm). Đoạn thẳng AO cắt đường tròn (O) tại M. Trên cung nhỏ MC của (O) lấy điểm D. AD cắt (O) tại điểm thứ hai E. I là trung điểm của DE. Đường thẳng qua D vuông góc với BO cắt BC tại H và cắt BE tại K.a) Chứng minh 4 điểm B, O, I, C cùng thuộc một đường trònb) Chứng minh...
Đọc tiếp
Cho đường tròn (O) và điểm A nằm ngoài đường tròn. Vẽ các tiếp tuyến AB và AC với đường tròn (B, C là các tiếp điểm). Đoạn thẳng AO cắt đường tròn (O) tại M. Trên cung nhỏ MC của (O) lấy điểm D. AD cắt (O) tại điểm thứ hai E. I là trung điểm của DE. Đường thẳng qua D vuông góc với BO cắt BC tại H và cắt BE tại K.
a) Chứng minh 4 điểm B, O, I, C cùng thuộc một đường tròn
b) Chứng minh góc ICB=góc IDK
c) Chứng minh H là trung điểm của DK
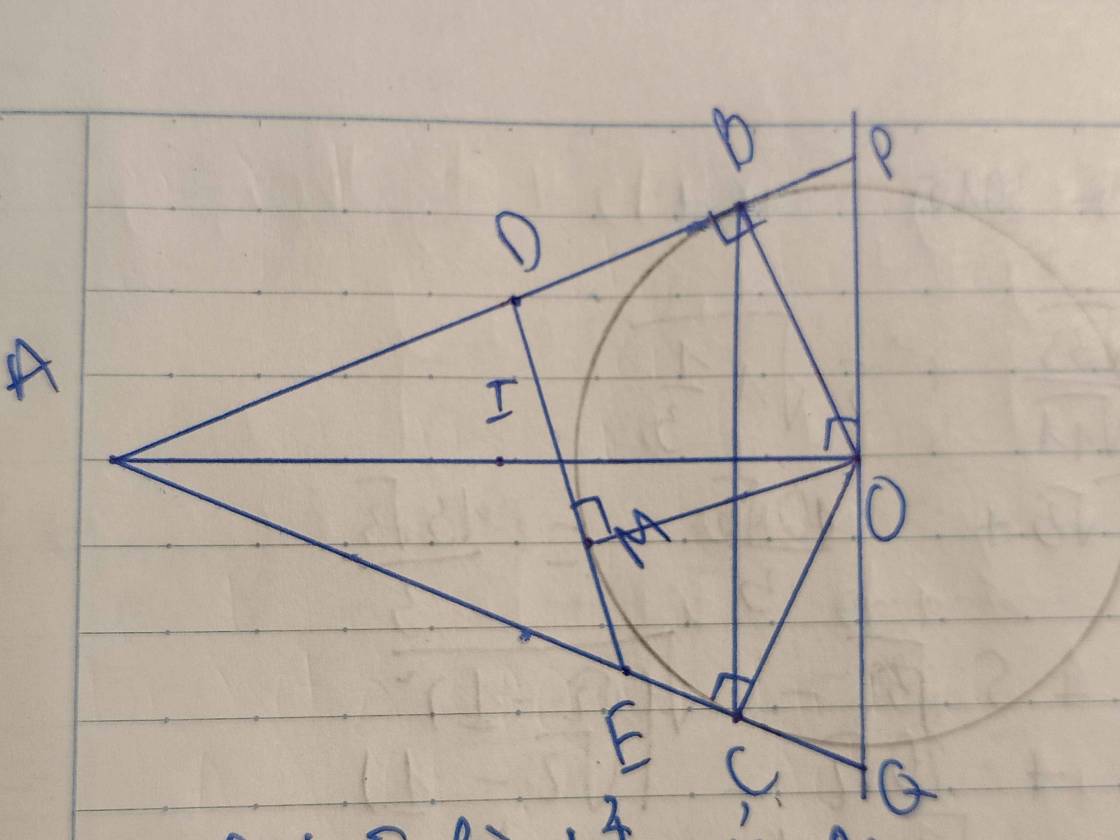
a) Xét tứ giác ABOC: ^ABO=^ACO=900 (Do AB và AC là 2 tiếp tuyến của (O))
=> Tứ giác ABOC nội tiếp đường tròn dường kính AO (1)
Ta có: DE là dây cung của (O), I là trung điểm DE => OI vuông góc DE => ^OIA=900
Xét tứ giác ABOI: ^ABO=^OIA=900 => Tứ giác ABOI nội tiếp đường tròn đường kính AO (2)
(1) + (2) => Ngũ giác ABOIC nội tiếp đường tròn
Hay 4 điểm B;O;I;C cùng thuộc 1 đường tròn (đpcm).
b) Gọi P là chân đường vuông góc từ D kẻ đến OB
Ta có: Tứ giác BOIC nội tiếp đường tròn => ^ICB=^IOP (Góc ngoài tại đỉnh đối) (3)
Dễ thấy tứ giác DIPO nội tiếp đường tròn đường kính OD
=> ^IOP=^IDP (=^IDK) (4)
(3) + (4) => ^ICB=^IDK (đpcm).
c) ^ICB=^IDK (cmt) => ^ICH=^IDH => Tứ giác DHIC nội tiếp đường tròn
=> ^DIH=^DCH hay ^DIH=^DCB.
Lại có: ^DCB=^DEB (2 góc nội tiếp cùng chắn cung BD) => ^DIH=^DEB
Mà 2 góc trên đồng vị => IH // EB hay IH // EK
Xét tam giác KDE: I là trung điểm DE (Dễ c/m); IH // EK; H thuộc DK
=> H là trung điểm DK (đpcm).