Giai hê phương trình sau
{3x-y(1+5x)=0
{x(1-5y)+y=0
giúp min vơi nha
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
24 tháng 9 2023
Tham khảo:
a) Vẽ đường thẳng \(\Delta : - 2x + y - 1 = 0\) đi qua hai điểm \(A(0;1)\) và \(B\left( { - 1; - 1} \right)\)
Xét gốc tọa độ \(O(0;0).\) Ta thấy \(O \notin \Delta \) và \( - 2.0 + 0 - 1 = - 1 < 0\)
Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng kể cả bờ \(\Delta \), chứa gốc tọa độ O
(miền không gạch chéo trên hình)
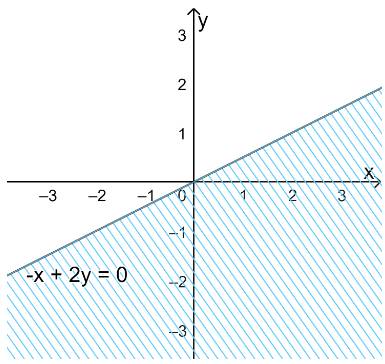
b) Vẽ đường thẳng \(\Delta : - x + 2y = 0\) đi qua hai điểm \(O(0;0)\) và \(B\left( {2;1} \right)\)
Xét điểm \(A(1;0).\) Ta thấy \(A \notin \Delta \) và \( - 1 + 2.0 = - 1 < 0\)
Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng không kể bờ \(\Delta \), không chứa điểm A (1;0)
(miền không gạch chéo trên hình)
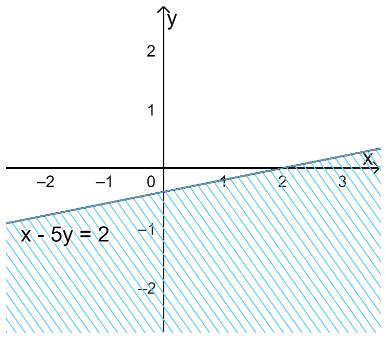
c) Vẽ đường thẳng \(\Delta :x - 5y = 2\) đi qua hai điểm \(A(2;0)\) và \(B\left( { - 3; - 1} \right)\)
Xét gốc tọa độ \(O(0;0).\) Ta thấy \(O \notin \Delta \) và \(0 - 5.0 = 0 < 2\)
Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng không kể bờ \(\Delta \), chứa gốc tọa độ O
(miền không gạch chéo trên hình)
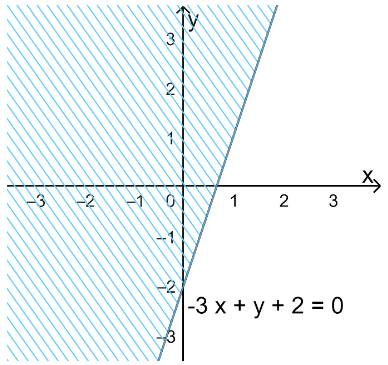
d) Vẽ đường thẳng \(\Delta : - 3x + y + 2 = 0\) đi qua hai điểm \(A(0; - 2)\) và \(B\left( {1;1} \right)\)
Xét điểm \(O(0;0).\) Ta thấy \(O \notin \Delta \) và \( - 3.0 + 0 + 2 = 2 > 0\)
Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng kể cả bờ \(\Delta \), không chứa điểm O (0;0)
(miền không gạch chéo trên hình)
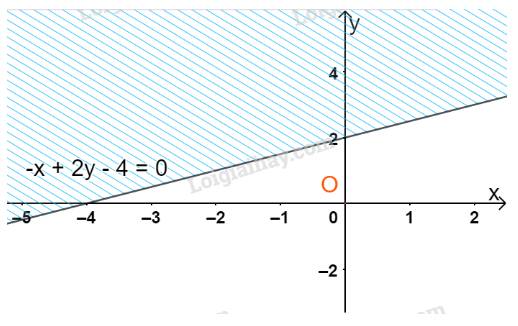
e) Ta có: \(3(x - 1) + 4(y - 2) < 5x - 3 \Leftrightarrow - 2x + 4y - 8 < 0 \Leftrightarrow - x + 2y - 4 < 0\)
Vẽ đường thẳng \(\Delta : - x + 2y -4 = 0\) đi qua hai điểm \(A(0;2)\) và \(B\left( {-4;0} \right)\)
Xét điểm \(O(0;0).\) Ta thấy \(O \notin \Delta \) và \( - 0 + 2.0 -4 = -4 < 0\)
Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng không kể bờ \(\Delta \), chứa điểm O (0;0)
(miền không gạch chéo trên hình)
6 tháng 3 2021
1) Ta có: \(x^2-4x+4=0\)
\(\Leftrightarrow\left(x-2\right)^2=0\)
\(\Leftrightarrow x-2=0\)
hay x=2
Vậy: S={2}
28 tháng 9 2021
\(a,\Leftrightarrow\left\{{}\begin{matrix}5x+15y=-10\\5x-4y=11\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}19y=-21\\5x-4y=11\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=-\dfrac{21}{19}\\5x-4\left(-\dfrac{21}{19}\right)=11\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{25}{19}\\y=-\dfrac{21}{19}\end{matrix}\right.\)
\(c,\Leftrightarrow\left\{{}\begin{matrix}3x+5y=1\\10x-5y=-40\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x+5y=1\\13x=-39\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-3\\y=2\end{matrix}\right.\\ d,\Leftrightarrow\left\{{}\begin{matrix}5x-10y=-30\\5x-3y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5x-3y=5\\-7y=-35\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=4\\y=5\end{matrix}\right.\\ e,\Leftrightarrow\left\{{}\begin{matrix}2\left(x+y\right)+3\left(x-y\right)=4\\2\left(x+y\right)+4\left(x-y\right)=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-y=6\\2\left(x+y\right)+3\cdot6=4\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x-y=6\\x+y=-7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{1}{2}\\y=-\dfrac{13}{2}\end{matrix}\right.\)
29 tháng 5 2015
a) a = 3; b = - 5 ; c = 2 => a + b + c = 0
=> PT có nghiệm là x = 1 ; và x = c/a = 2/3
b) từ PT thứ hai => x = -5y. thế x = -5y vào PT thứ nhất
=> 3.(-5y) - 4y = 1 <=> -15y - 4y = 1 <=> -19y = 1 <=> y = \(-\frac{1}{19}\) => x = (-5).(\(-\frac{1}{19}\)) = \(\frac{5}{19}\)
Vậy nghiệm của hệ là: (x;y) = (\(\frac{5}{19}\); \(-\frac{1}{19}\) )
3 tháng 2 2016
Ta có: a=3; b= -5; c= 2
Δ=b^2 - 4ac = -5^2 - 4.3.2
= 25 - 24 = 1
Vì Δ > 0 nên pt có 2 nghiệm phân biệt
\(x_1=\frac{5-\sqrt[]{1}}{2.3}\) = \(\frac{2}{3}\)
\(X_2=_{ }\frac{5+\sqrt{1}}{2.3}\) =1
4 tháng 1
a: \(\left\{{}\begin{matrix}3x-2y=11\\4x-5y=3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3x=11+2y\\4x-5y=3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{2}{3}y+\dfrac{11}{3}\\4\left(\dfrac{2}{3}y+\dfrac{11}{3}\right)-5y=3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{2}{3}y+\dfrac{11}{3}\\\dfrac{8}{3}y+\dfrac{44}{3}-5y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{2}{3}y+\dfrac{11}{3}\\-\dfrac{7}{3}y=3-\dfrac{44}{3}=-\dfrac{35}{3}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=5\\x=\dfrac{2}{3}\cdot5+\dfrac{11}{3}=\dfrac{10}{3}+\dfrac{11}{3}=\dfrac{21}{3}=7\end{matrix}\right.\)
b: \(\left\{{}\begin{matrix}\dfrac{x}{2}-\dfrac{y}{3}=1\\5x-8y=3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{x}{2}=\dfrac{y}{3}+1\\5x-8y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{2}{3}y+2\\5\left(\dfrac{2}{3}y+2\right)-8y=3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{2}{3}y+2\\\dfrac{10}{3}y+10-8y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-\dfrac{14}{3}y=3-10=-7\\x=\dfrac{2}{3}y+2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=7:\dfrac{14}{3}=7\cdot\dfrac{3}{14}=\dfrac{3}{2}\\x=\dfrac{2}{3}\cdot\dfrac{3}{2}+2=3\end{matrix}\right.\)
c: \(\left\{{}\begin{matrix}3x+5y=1\\2x-y=-8\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=2x+8\\3x+5\left(2x+8\right)=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=2x+8\\3x+10x+40=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=2x+8\\13x=-39\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-3\\y=2\cdot\left(-3\right)+8=8-6=2\end{matrix}\right.\)
d: \(\left\{{}\begin{matrix}\dfrac{x}{y}=\dfrac{2}{3}\\x+y-10=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{2}{3}y\\x+y=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2}{3}y+y=10\\x=\dfrac{2}{3}y\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{5}{3}y=10\\x=\dfrac{2}{3}y\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=6\\x=\dfrac{2}{3}\cdot6=4\end{matrix}\right.\)
10 tháng 10 2023
Chọn a: \(x+5y+2\le0\) là bất phương trình bậc nhất 2 ẩn.
18 tháng 4 2020
1a) 7x + 21 = 0
<=> 7x = -21
<=> x = -21/7
<=> x = -3
Vậy nghiệm của phương trình trên là S = {-3}
b) 12 - 6x = 0
<=> -6x = -12
<=> x = -12/-6
<=> x = 2
Vậy nghiệm của phương trình trên là S = {2}
c) 5x - 2 = 0
<=> 5x = 2
<=> x = 2/5
Vậy nghiệm của phương trình trên là S = {2/5}
d) -2x + 14 = 0
<=> -2x = -14
<=> x = -14/-2
<=> x = 7
Vậy nghiệm của phương trình là S = {7}
e) 0,25x + 1,5 = 0
<=> 0,25x = -1,5
<=> x = -1,5/0,25
<=> x = -6
Vậy nghiệm của phương trình là S = {-6}
2a) 3x + 1 = 7x - 11
<=> 3x - 7x = -11 - 1
<=> -4x = -12
<=> x = -12/-4
<=> x = 3
Vậy nghiệm của phương trình trên là S = {3}
b) 11 - 2x = x - 1
<=> -2x - x = -1 - 11
<=> -3x = -12
<=> x = -12/-3
<=> x = 4
Vậy nghiệm của phương trình là S = {4}
c) 5 - 3x = 6x + 7
<=> -3x - 6x = 7 - 5
<=> -9x = 2
<=> x = 2/-9
Vậy nghiệm của phương trình trên là S = {-2/9}
d) 15 - 8x = 9 - 5x
<=> -8x + 5x = 9 - 15
<=> -3x = 6
<=> x = 6/-3
<=> x = -2
Vậy nghiệm của phương trình trên là S = {-2}
~Sai thì thôi
#Học tốt!!!
~NTTH~
\(\hept{\begin{cases}3x-y\left(5x+1\right)=0\\x\left(1-5y\right)+y=0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}3x-5xy-y=0\\x-5xy+y=0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}4x-10xy=0\\x-5xy+y=0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}4x\left(1-\frac{5}{2}y\right)=0\\x-5xy+y=0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=0;\frac{5}{2}y=1\\x-5xy+y=0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}y=\frac{2}{5}\\-5.\frac{2}{5}x+\frac{2}{5}=0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}y=\frac{2}{5}\\x=\frac{1}{5}\end{cases}}\)
vậy hệ phương trình có nghiệm duy nhất \(\left(x;y\right)=\left(\frac{1}{5};\frac{2}{5}\right)\)
mình giống Despacito