Cho M = -x2 - y2 + xy + 2x + 2y
Tìm cặp số x, y để biểh thức đạt GTLN và tìm giá trị đó
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HS
1
18 tháng 5 2019
A=-x^2-y^2+2x+2y+xy
A= -( x^2+y^2-2x-2y-xy)
A=-[( x^2-2.x.(y/2+1)+(y/2+1)^2+(3y^2/4- 3y+3)-4]
A= -[(x-y/2-1)^2+ 3.(y/2-1)^2+4)]
Tự làm nốt nhé
CM
2 tháng 10 2017
Đáp án C
Tọa độ giao điểm của hai đồ thị là nghiệm của phương trình
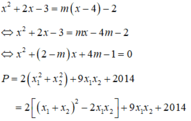
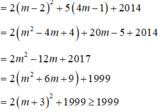
Dấu “=” xảy ra khi và chỉ khi m = -3
CM
25 tháng 6 2018
Theo đầu bài ta có: log 2x+ log2y=log4(x+y) hay 2 log 2(xy) =log2(x+y)
Suy ra x+y=(xy) 2
Đặt u= x+ y; v= xy ta có điều kiện u2-4v≥0; u>0; v>0 .
Mà 
Ta có
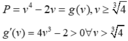
nên minP=
2
4
3
khi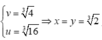 
Chọn A.
-M = x^2+y^2-xy-2x-2y
-4M = 4x^2+4y^2-4xy-8x-8y
= [ (4x^2-4xy+y^2) - 2.(2x-y).2 + 4 ] + (3y^2-12y+12)-16
= [ (2x-y)^2 - 2.(2x-y).2 + 4 ] + 3.(y^2-4y+4) - 16
= (2x-y-2)^2 + 3.(y-2)^2 - 16 >= -16 => M < = 4
Dấu "=" xảy ra <=> 2x-y-2 = 0 và y-2 = 0 <=> x = y = 2
Vậy ............
Tk mk nha