Cho tam giác ABC là tam giác đều có AB=3cm. Tính diện tích tam giác ABC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

nếu gọi canh là 'a' thì diện tích của tam giác đều là:
(a2*căn 3)/4
do đó diện tích bằng (32*căn 3)/4
hãy k đúng cho mình nha

![]()
Suy ra: tam giác ABC vuông tại A.
Diện tích tam giác ABC là:
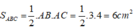
*Gọi tam giác ABC đồng dạng với tam giác MNP theo tỉ số k
Suy ra:
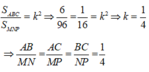
Thay số
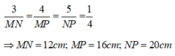
Chọn đáp án B

\(\dfrac{1}{2}\cdot AB\cdot AC\cdot sinA=6\)
=>1/2*3*sin135*AB=6
=>\(AB=4\sqrt{2}\left(cm\right)\)

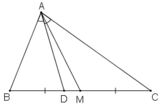
a) Ta có: 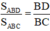 (do hai tam giác có chung chiều cao từ đỉnh A)
(do hai tam giác có chung chiều cao từ đỉnh A)
ΔABC có AD là phân giác
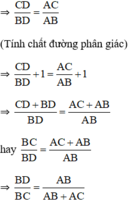
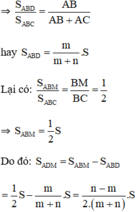
b) Với n = 7; m = 3, thay vào kết quả phần a ta có:
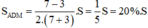
Vậy diện tích tam giác ADM chiếm 20% diện tích tam giác ABC.

\(S_{AHC}=\dfrac{AH\cdot HC}{2}=\dfrac{2.4\cdot3.2}{2}=2.4\cdot1.6=3.84\left(cm^2\right)\)
Xét \(\Delta ABC\) vuông tại A có
\(BC^2=AB^2+AC^2=25\)
\(\Rightarrow BC=5\left(cm\right)\)
AC\(^2\) = CH . CB = 5 CH
\(\Rightarrow CH=3,2\left(cm\right)\)
AB . AC = AH . BC \(\Rightarrow AH=2,4\)
Nên \(S_{AHC}=\dfrac{1}{2}.AH.CH=\dfrac{1}{2}.2,4.3,2=3,84\left(cm^2\right)\)
diện tích = 3x3=9(cm2)
Đáp số : 9 cm2
chúc bạn học tốt
cho tam giác ABC có 3 cạnh là A ;B :;C tỉ lệ với 3;4;5 . tính độ dài của tam giác . biết cạnh lớn nhất lớn hơn cạnh nhỏ nhất là 6cm