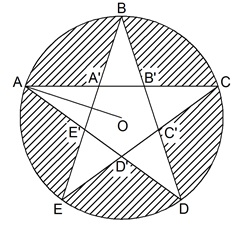
Cho hình sao đều 5 cánh ABCDE, các cạnh giao nhau tại A’, B’, C’, D’, E’. Đường tròn ngoại tiếp hình sao ABCDE có bán kính OA = R = 18. Tính tổng: AC + AB’ + AA’ + A’B’ (Làm tròn kết quả đến 4 chữ số ở phần thập phân)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
9 tháng 3 2019
Đề không ghi rõ các giao điểm A',B',C',D',E' xác định như thế nào nên mình quy ước như sau:
AC cắt BE tại A'
AD cắt BE tại B'
AD cắt CE tại C'
BD cắt CE tại D'
BD cắt AC tại E'
Hình trong này hơi khó vẽ nên bạn tự vẽ hình đi nhé.
Bạn nên vẽ ngũ giác A'B'C'E'D' đều trước, rồi vẽ hình sao ABCDE sau (bằng cách kéo dài các cạnh để chúng cắt nhau)
Các bước giải bài toán:
+Chứng minh các tam giác A'B'A, B'C'E, C'D'D, D'E'C, E'A'B bằng nhau .
+Từ đó suy ra AC + AB' + AA' + A'B' = 2AC => Bài toán quy về tính AC
+Tính các góc trong ngũ giác -> trong tam giác -> góc OAC = 18 độ
+Tiếp theo bạn dùng tỉ lượng giác để tính cạnh AC khi đã biết OA=18 và góc OAC=18 độ.Bạn sẽ hạ OH vuông góc AC. Đây là kiến thức lớp 9. Do đó nếu cần bạn có thể kiểm tra và ghi rõ lại đề!
Đáp án: 60,8676
Chúc bạn học tốt.
9 tháng 3 2019
Xin lỗi bạn mình nhầm một xí, đáp án đúng của bài toán phải là: 68,4761.
Mình bấm máy tính như sau: 2*2*18*cos(18)
HQ
Hà Quang Minh
Giáo viên
23 tháng 9 2023
Áp dụng định lí cosin trong tam giác ABC ta có:
\(B{C^2} = A{C^2} + A{B^2} - 2AC.AB.\cos A\)
\(\begin{array}{l} \Leftrightarrow B{C^2} = 7,{5^2} + 3,{5^2} - 2.7,5.3,5.\cos {135^o}\\ \Leftrightarrow B{C^2} \approx 105,6\\ \Leftrightarrow BC \approx 10,3\end{array}\)
Áp dụng định lí sin trong tam giác ABC ta có: \(\frac{{BC}}{{\sin A}} = 2R\)
\( \Rightarrow R = \frac{{BC}}{{2.\sin A}} = \frac{{10,3}}{{2.\sin {{135}^o}}} \approx 7,3\)
25 tháng 12 2023
a: Xét (O) có
AB,AC là các tiếp tuyến
Do đó: AB=AC và AO là phân giác của góc BAC
Ta có: AB=AC
=>A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OA là đường trung trực của BC
=>OA\(\perp\)BC tại H và H là trung điểm của BC
Xét ΔBOA vuông tại B có \(cosBOA=\dfrac{BO}{OA}=\dfrac{1}{2}\)
nên \(\widehat{BOA}=60^0\)
Xét ΔBOA vuông tại B có BH là đường cao
nên \(OH\cdot OA=OB^2\)
=>\(OH\cdot2R=R^2\)
=>\(OH=\dfrac{R^2}{2R}=\dfrac{R}{2}\)
b: Ta có: \(\widehat{ABM}+\widehat{OBM}=\widehat{OBA}=90^0\)
\(\widehat{HBM}+\widehat{OMB}=90^0\)(ΔHMB vuông tại H)
mà \(\widehat{OBM}=\widehat{OMB}\)
nên \(\widehat{ABM}=\widehat{HBM}\)
=>BM là phân giác của góc ABH
Xét ΔABC có
BM,AM là các đường phân giác
BM cắt AM tại M
Do đó: M là tâm đường tròn nội tiếp ΔABC
mk chịu