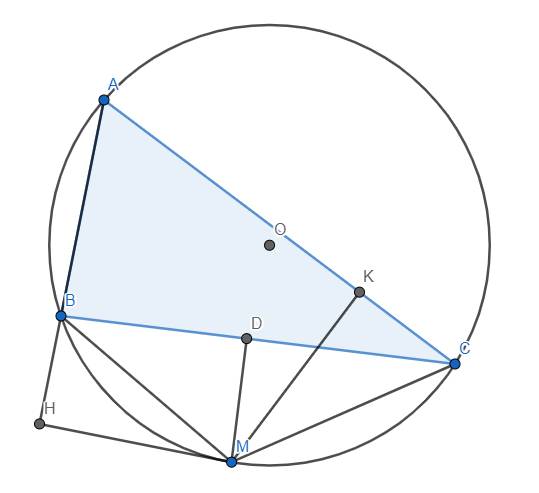
cho ΔABC có ba góc nhọn nội tiếp trong đường tròn tâm O . gọi M là điểm bất kỳ trên cung nhỏ AC . gọi E và F lần lượt là chân các đường vuông kẻ từ M đến BC và AC. P là trung điểm AB, Q là trng điểm của FE
a/ cm MFEC nội tiếp
b/ cm BM.È=BA.ME
c/cm ΔAMP∼ΔFMQ
d/ cm ∠PQM=90

a) Ta có: \(\angle MFC=\angle MEC=90\Rightarrow MFEC\) nội tiếp
b) Ta có: \(\angle MFE=180-\angle MCE=\angle MAB\)
\(\angle FME=\angle FCE=\angle AMB\)
Xét \(\Delta AMB\) và \(\Delta MFE\):Ta có: \(\left\{{}\begin{matrix}\angle MFE=\angle MAB\\\angle FME=\angle AMB\end{matrix}\right.\)
\(\Rightarrow\Delta AMB\sim\Delta MFE\left(g-g\right)\Rightarrow\dfrac{BM}{BA}=\dfrac{ME}{FE}\Rightarrow BM.FE=ME.BA\)
c) Ta có: \(\Rightarrow\Delta AMB\sim\Delta MFE\Rightarrow\dfrac{MF}{FE}=\dfrac{MA}{AB}\Rightarrow2\dfrac{MF}{FE}=2\dfrac{MA}{AB}\)
\(\Leftrightarrow\dfrac{MF}{FQ}=\dfrac{MA}{AB}\)
Xét \(\Delta AMP\) và \(\Delta FMQ\):Ta có: \(\left\{{}\begin{matrix}\angle MFQ=\angle MAP\\\dfrac{MF}{FQ}=\dfrac{MA}{MB}\end{matrix}\right.\)
\(\Rightarrow\Delta AMP\sim\Delta FMQ\left(c-g-c\right)\)
d) Kẻ \(MD\bot AB\left(D\in AB\right)\)
Ta có: \(\angle MDA+\angle MFA=90+90=180\Rightarrow\) MDAF nội tiếp
\(\Rightarrow\angle DFA=\angle DMA=90-\angle DAM\)
Tương tự \(\Rightarrow\angle EFC=\angle EMC=90-\angle MCB\)
mà \(\angle DAM=\angle MCB\) (AMCB nội tiếp)\(\Rightarrow\angle DFA=\angle EFC\)
mà A,F,C thẳng hàng \(\Rightarrow\) \(\)D,F,E thẳng hàng
Ta có: \(\angle MQF=\angle MPA\left(\Delta MFQ\sim\Delta MAP\right)\Rightarrow\angle MQD=\angle MPD\)
\(\Rightarrow\) MDPQ nội tiếp mà \(\angle MDP=90\Rightarrow\angle PQM=90\)