x^3-9x^2+6x+16=0 tìm x
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) \(5x\left(x-4\right)-x^2+16=0\)
\(4x^2-20x+16=0\)
\(\Rightarrow\orbr{\begin{cases}x=4\\x=1\end{cases}}\)
b) \(x+6x^2+9x^2=0\)
\(x\left(3x+1\right)^2=0\)
\(\Rightarrow\orbr{\begin{cases}x=0\\x=-\frac{1}{3}\end{cases}}\)

a) x4 - 16x2 = 0
<=> ( x2 )2 - ( 4x )2 = 0
<=> ( x2 - 4x )( x2 + 4x ) = 0
<=> [ x( x - 4 ) ][ x( x + 4 ) ] = 0
<=> x( x - 4 )x( x + 4 ) = 0
<=> x2( x - 4 )( x + 4 ) = 0
<=> \(\hept{\begin{cases}x^2=0\\x-4=0\\x+4=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=0\\x=\pm4\end{cases}}\)( thay bằng dấu hoặc hộ mình nhé )
b) 9x2 + 6x + 1 = 0
<=> ( 3x )2 + 2.3x.1 + 12 = 0
<=> ( 3x + 1 )2 = 0
<=> 3x + 1 = 0
<=> 3x = -1
<=> x = -1/3
c) x2 - 6x = 16
<=> x2 - 6x - 16 = 0
<=> x2 + 2x - 8x - 16 = 0
<=> x( x + 2 ) - 8( x + 2 ) = 0
<=> ( x + 2 )( x - 8 ) = 0
<=> \(\orbr{\begin{cases}x+2=0\\x-8=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=-2\\x=8\end{cases}}\)
d) 9x2 + 6x = 80
<=> 9x2 + 6x - 80 = 0
<=> 9x2 + 30x - 24x - 80 = 0
<=> 9x( x + 10/3 ) - 24( x + 10/3 ) = 0
<=> ( x + 10/3 )( 9x - 24 ) = 0
<=> \(\orbr{\begin{cases}x+\frac{10}{3}=0\\9x-24=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=-\frac{10}{3}\\x=\frac{8}{3}\end{cases}}\)
e) Áp dụng công thức an.bn = ( ab )n ta có :
25( 2x - 1 )2 - 9( x + 1 )2 = 0
<=> 52( 2x - 1 )2 - 32( x + 1 )2 = 0
<=> [ 5( 2x - 1 ) ]2 - [ 3( x + 1 ) ]2 = 0
<=> ( 10x - 5 )2 - ( 3x + 3 )2 = 0
<=> [ ( 10x - 5 ) - ( 3x + 3 ) ][ ( 10x - 5 ) + ( 3x + 3 ) ] = 0
<=> ( 10x - 5 - 3x - 3 )( 10x - 5 + 3x + 3 ) = 0
<=> ( 7x - 8 )( 13x - 2 ) = 0
<=> \(\orbr{\begin{cases}7x-8=0\\13x-2=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=\frac{8}{7}\\x=\frac{2}{13}\end{cases}}\)
Bài làm :
a) x4 - 16x2 = 0
<=> ( x2 )2 - ( 4x )2 = 0
<=> ( x2 - 4x )( x2 + 4x ) = 0
<=> [ x( x - 4 ) ][ x( x + 4 ) ] = 0
<=> x( x - 4 )x( x + 4 ) = 0
<=> x2( x - 4 )( x + 4 ) = 0
Vậy x=0 hoặc x=±4
b) 9x2 + 6x + 1 = 0
<=> ( 3x )2 + 2.3x.1 + 12 = 0
<=> ( 3x + 1 )2 = 0
<=> 3x + 1 = 0
<=> 3x = -1
<=> x = -1/3
c) x2 - 6x = 16
<=> x2 - 6x - 16 = 0
<=> x2 + 2x - 8x - 16 = 0
<=> x( x + 2 ) - 8( x + 2 ) = 0
<=> ( x + 2 )( x - 8 ) = 0
\(\Leftrightarrow\orbr{\begin{cases}x+2=0\\x-8=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=-2\\x=8\end{cases}}\)
d) 9x2 + 6x = 80
<=> 9x2 + 6x - 80 = 0
<=> 9x2 + 30x - 24x - 80 = 0
<=> 9x( x + 10/3 ) - 24( x + 10/3 ) = 0
<=> ( x + 10/3 )( 9x - 24 ) = 0
\(\Leftrightarrow\orbr{\begin{cases}x+\frac{10}{3}=0\\9x-24=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=-\frac{10}{3}\\x=\frac{8}{3}\end{cases}}\)
e) 25( 2x - 1 )2 - 9( x + 1 )2 = 0
<=> 52( 2x - 1 )2 - 32( x + 1 )2 = 0
<=> [ 5( 2x - 1 ) ]2 - [ 3( x + 1 ) ]2 = 0
<=> ( 10x - 5 )2 - ( 3x + 3 )2 = 0
<=> [ ( 10x - 5 ) - ( 3x + 3 ) ][ ( 10x - 5 ) + ( 3x + 3 ) ] = 0
<=> ( 10x - 5 - 3x - 3 )( 10x - 5 + 3x + 3 ) = 0
<=> ( 7x - 8 )( 13x - 2 ) = 0
\(\Leftrightarrow\orbr{\begin{cases}7x-8=0\\13x-2=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=\frac{8}{7}\\x=\frac{2}{13}\end{cases}}\)

a) Ta có : x4 - 16x2 = 0
=> x4 - 8x2 - 8x2 + 64 = 64
=> x2(x2 - 8) - 8(x2 - 8) = 64
=> (x2 - 8)2 = 64
=> \(\orbr{\begin{cases}x^2-8=8\\x^2-8=-8\end{cases}}\Rightarrow\orbr{\begin{cases}x^2=16\\x^2=0\end{cases}}\Rightarrow\orbr{\begin{cases}x=\pm4\\x=0\end{cases}}\Rightarrow x\in\left\{4;-4;0\right\}\)
b) Ta có 9x2 + 6x + 1 = 0
=> 9x2 + 3x + 3x + 1 = 0
=> 3x(3x + 1) + (3x + 1) = 0
=> (3x + 1)2 = 0
=> 3x + 1 = 0
=> x = -1/3
c) Ta có x2 - 6x = 16
=> x2 - 6x + 9 = 25
=> (x - 3)2 = 25
=> \(\orbr{\begin{cases}x-3=5\\x-3=-5\end{cases}}\Rightarrow\orbr{\begin{cases}x=8\\x=-2\end{cases}}\Rightarrow x\in\left\{8;-2\right\}\)
d) 9x2 + 6x = 80
=> 9x2 + 6x + 1 = 81
=> (3x + 1)2 = 81
=> \(\orbr{\begin{cases}3x+1=9\\3x+1=-9\end{cases}}\Rightarrow\orbr{\begin{cases}x=\frac{8}{3}\\x=-\frac{10}{3}\end{cases}\Rightarrow x\in}\left\{\frac{8}{3};\frac{-10}{3}\right\}\)
e) 25(2x - 1)2 - 9(x + 1)2 = 0
=> [5(2x - 1)]2 - [3(x + 1)]2 = 0
=> (10x - 5)2 - (3x + 3)2 = 0
=> (10x - 5 - 3x - 3)(10x - 5 + 3x + 3) = 0
=> (7x - 8)(13x - 2) = 0
=> \(\orbr{\begin{cases}7x=8\\13x=2\end{cases}}\Rightarrow\orbr{\begin{cases}x=\frac{8}{7}\\x=\frac{2}{13}\end{cases}}\)

\(x^3-9x+7x^2-63=0\)
\(\Rightarrow\left(x^3+7x^2\right)-9x-63=0\)
\(\Rightarrow x^2\left(x+7\right)-9\left(x+7\right)=0\)
\(\Rightarrow\left(x^2-9\right)\left(x+7\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x^2-9=0\\x+7=0\end{cases}\Rightarrow\orbr{\begin{cases}x^2=9\\x=-7\end{cases}\Rightarrow}\orbr{\begin{cases}x=\pm3\\x=-7\end{cases}}}\)
Vậy ...
x3−9x+7x2−63=0x3−9x+7x2−63=0
⇒(x3+7x2)−9x−63=0⇒(x3+7x2)−9x−63=0
⇒x2(x+7)−9(x+7)=0⇒x2(x+7)−9(x+7)=0
⇒(x2−9)(x+7)=0⇒(x2−9)(x+7)=0
⇒{x2−9=0x+7=0⇒{x2=9x=−7⇒{x=±3x=−7⇒{x2−9=0x+7=0⇒{x2=9x=−7⇒{x=±3x=−7
Vậy ...

a) <=> 4x^3 - 12x^2 - x^2 + 3x + 6x - 18 = 0
<=> 4x^2 (x - 3) - x(x - 3) + 6(x - 3) = 0
<=> (x - 3)(4x^2 - x + 6) = 0
xét 2 th
. x - 3 = 0 <=> x = 3
. 4x^2 - x + 6 = 0
<=> 4x^2 + 2.(1/2)x + 1/4 + 23/4 = 0
<=> (4x + 1/2)^2 = -23/4
.... phần sau bạn tự làm nhé
vậy pt trên có nghiệm là ...
. mik bận nên chỉ làm như vậy thôi.. những ý sau thì tách tương tự
c) => x3 + 2x2 - 6x2 - 12x + 4x + 8 = 0
=> (x3 + 2x2) - (6x2 + 12x) + (4x + 8) = 0
=> x2. (x +2) - 6x. (x + 2) + 4.(x + 2) =0
=> (x +2).(x2 - 6x + 4) = 0
=> x+ 2 = 0 hoặc x2 - 6x + 4 = 0
+) x+ 2 =0 => x = -2
+) x2 - 6x + 4 = 0 => x2 - 2.x.3 + 9 - 5 = 0 => (x -3)2 = 5
=> x - 3 = \(\sqrt{5}\) hoặc x - 3 = - \(\sqrt{5}\)
=> x = 3 + \(\sqrt{5}\) hoặc x = 3 - \(\sqrt{5}\)
vậy...

1/ \(x^3-7x+6=0\)
\(\Leftrightarrow x^3+3x^2-3x^2-9x+2x+6=0\)
\(\Leftrightarrow x^2\left(x+3\right)-3x\left(x+3\right)+2\left(x+3\right)=0\)
\(\Leftrightarrow\left(x+3\right)\left(x^2-3x+2\right)=0\)
\(\Leftrightarrow\left(x+3\right)\left(x^2-x-2x+2\right)=0\)
\(\Leftrightarrow\left(x+3\right)\left[x\left(x-1\right)+2\left(x-1\right)\right]=0\)
\(\Leftrightarrow\left(x+3\right)\left(x-1\right)\left(x+2\right)=0\)
\(\Leftrightarrow\)\(x+3=0\)
hoặc \(x-1=0\)
hoặc \(x+2=0\)
\(\Leftrightarrow\)\(x=-3\)
hoặc \(x=1\)
hoặc \(x=-2\)
Vậy tập nghiệm của phương trình là : \(S=\left\{-3;1;-2\right\}\)
2/ \(x^3-6x^2-x+30\)
\(\Leftrightarrow x^3+2x^2-8x^2-16x+15x+30=0\)
\(\Leftrightarrow x^2\left(x+2\right)-8x\left(x+2\right)+15\left(x+2\right)=0\)
\(\Leftrightarrow\left(x+2\right)\left(x^2-8x+15\right)=0\)
\(\Leftrightarrow\left(x+2\right)\left(x^2-3x-5x+15\right)=0\)
\(\Leftrightarrow\left(x+2\right)\left[x\left(x-3\right)-5\left(x-3\right)\right]=0\)
\(\Leftrightarrow\left(x+2\right)\left(x-3\right)\left(x-5\right)=0\)
\(\Leftrightarrow\)\(x+2=0\)
hoặc \(x-3=0\)
hoặc \(x-5=0\)
\(\Leftrightarrow\)\(x=-2\)
hoặc \(x=3\)
hoặc \(x=5\)
Vậy tập nghiệm của phương trình là :\(S=\left\{-2;3;5\right\}\)
3/ \(x^3-9x^2+6x+16=0\)
\(\Leftrightarrow x^3+x^2-10x^2-10x+16x+16=0\)
\(\Leftrightarrow x^2\left(x+1\right)-10x\left(x+1\right)+16\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^2-10x+16\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^2-8x-2x+16\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left[x\left(x-8\right)-2\left(x-8\right)\right]=0\)
\(\Leftrightarrow\left(x+1\right)\left(x-8\right)\left(x-2\right)=0\)
\(\Leftrightarrow\)\(x+1=0\)
hoặc \(x-8=0\)
hoặc \(x-2=0\)
\(\Leftrightarrow\)\(x=-1\)
hoặc \(x=8\)
hoặc \(x=2\)
Vậy tập nghiệm của phương trình là :\(S=\left\{-1;8;2\right\}\)
4/ Đề bài sai ! Sửa lại nhé :
\(2x^3-x^2+5x+3=0\)
\(\Leftrightarrow2x^3+x^2-2x^2-x+6x+3=0\)
\(\Leftrightarrow x^2\left(2x+1\right)-x\left(2x+1\right)+3\left(2x-1\right)=0\)
\(\Leftrightarrow\left(2x+1\right)\left(x^2-x+3\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}2x+1=0\\x^2-x+3=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=-\frac{1}{2}\left(tm\right)\\\left(x-\frac{1}{2}\right)^2+\frac{11}{4}=0\left(ktm\right)\end{cases}}\)
Vậy tập nghiệm của phương trình là : \(S=\left\{-\frac{1}{2}\right\}\)

d: Ta có: \(9x^2+6x-8=0\)
\(\Leftrightarrow9x^2+12x-6x-8=0\)
\(\Leftrightarrow\left(3x+4\right)\left(3x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{4}{3}\\x=\dfrac{2}{3}\end{matrix}\right.\)
e: Ta có: \(x\left(x-2\right)+x-2=0\)
\(\Leftrightarrow\left(x-2\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\)
f: Ta có: \(5x\left(x-3\right)-x+3=0\)
\(\Leftrightarrow\left(x-3\right)\left(5x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=\dfrac{1}{5}\end{matrix}\right.\)

1, \(x^3+4x^2+4x=0\Leftrightarrow x\left(x^2+4x+4\right)=0\)
\(\Leftrightarrow x\left(x+2\right)^2=0\Leftrightarrow x=-2;x=0\)
2, \(\left(x+3\right)^2-4=0\Leftrightarrow\left(x+3-2\right)\left(x+3+2\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+5\right)=0\Leftrightarrow x=-5;x=1\)
3, \(x^4-9x^2=0\Leftrightarrow x^2\left(x^2-9\right)=0\)
\(\Leftrightarrow x^2\left(x-3\right)\left(x+3\right)=0\Leftrightarrow x=0;\pm3\)
4, \(x^2-6x+9=81\Leftrightarrow\left(x-3\right)^2=9^2\)
\(\Leftrightarrow\left(x-3-9\right)\left(x-3+9\right)=0\Leftrightarrow\left(x-12\right)\left(x+6\right)=0\Leftrightarrow x=-6;x=12\)
5, em xem lại đề nhé
à lag tý @@
5, \(x^3+6x^2+9x-4x=0\Leftrightarrow x^3+6x^2+5x=0\)
\(\Leftrightarrow x\left(x^2+6x+5\right)=0\Leftrightarrow x\left(x^2+x+5x+5\right)=0\)
\(\Leftrightarrow x\left(x+1\right)\left(x+5\right)=0\Leftrightarrow x=-5;x=-1;x=0\)
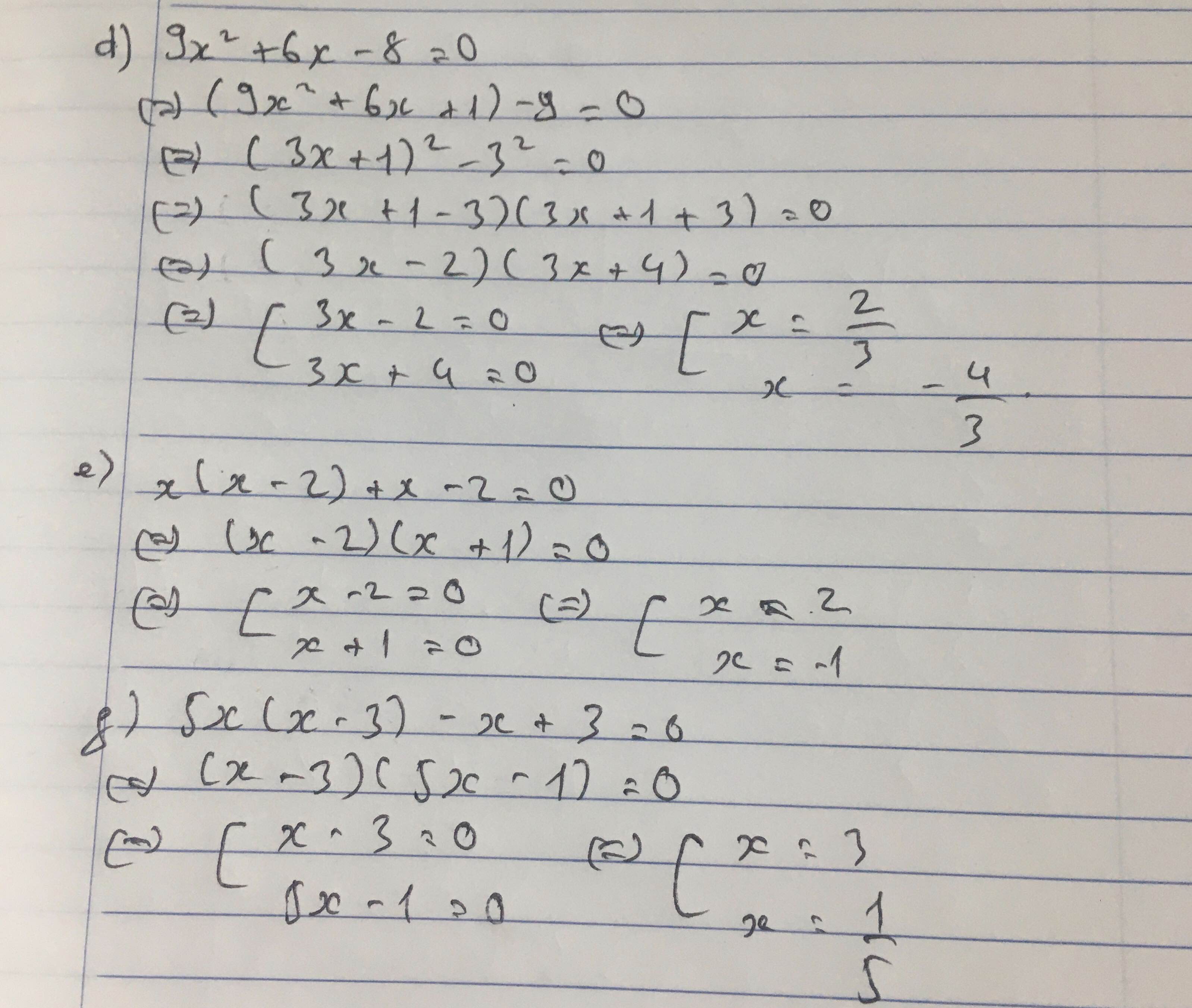 Mình trình bày trong hình ^^ Bn tham khảo nhé
Mình trình bày trong hình ^^ Bn tham khảo nhé
x^3-9x^2+6x+16=0
<=>x3-10x2+16x+x2-10x+16=0
<=>x.(x2-10x+16)+(x-2)(x-8)=0
<=>x.(x-2)(x-8)+(x-2)(x-8)=0
<=>(x-2)(x-8)(x+1)=0
<=>x=2 hoặc x=8 hoặc x=-1