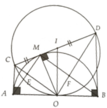
Cho đường tròn (O) có hai đường kính AB, CD không vuông góc với nhau.
a) Chứng minh: tứ giác ACBD là hình chữ nhật.
b) Tiếp tuyến tại A của đường tròn (O) cắt các đường thẳng BC, BD lần lượt tại E, F. Chứng minh: tứ giác ECDF nội tiếp.
c) Từ C và D vẽ các tiếp tuyến với đường tròn (O) cắt EF theo thứ tự tại M và N. Chứng minh: MN=12EF.
d) Gọi I là chân đường vuông góc hạ từ M xuống BN; H là giao điểm của AB và MI. Chứng minh: HA = HO.