Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
Do đó: ΔAMB=ΔAMC
=>\(\widehat{AMB}=\widehat{AMC}\)
mà \(\widehat{AMB}+\widehat{AMC}=180^0\)(hai góc kề bù)
nên \(\widehat{AMB}=\widehat{AMC}=\dfrac{180^0}{2}=90^0\)
b: Xét ΔMBA vuông tại M và ΔMCD vuông tại M có
MB=MC
MA=MD
Do đó: ΔMBA=ΔMCD
=>\(\widehat{MBA}=\widehat{MCD}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//CD
c: Xét ΔBEM vuông tại E và ΔCFM vuông tại F có
MB=MC
\(\widehat{MBE}=\widehat{MCF}\)
Do đó: ΔBEM=ΔCFM
=>ME=MF
ΔBEM=ΔCFM
=>\(\widehat{BME}=\widehat{CMF}\)
mà \(\widehat{BME}+\widehat{EMC}=180^0\)(hai góc kề bù)
nên \(\widehat{CMF}+\widehat{EMC}=180^0\)
=>F,M,E thẳng hàng
mà MF=ME
nên M là trung điểm của EF
a: Xét ΔAMB và ΔAMC có
AM chung
\(\widehat{BAM}=\widehat{CAM}\)
AB=AC
Do đó: ΔABM=ΔACM
a: Ta có: ΔABC cân tại A
mà AM là đường phân giác
nên M là trung điểm của BC
hay MB=MC
a: Xét ΔMAB và ΔMDC có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)(hai góc đối đỉnh)
MB=MC
Do đó: ΔMAB=ΔMDC
=>\(\widehat{MAB}=\widehat{MDC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//CD
b: Xét ΔEMB vuông tại E và ΔFMC vuông tại F có
MB=MC
\(\widehat{EMB}=\widehat{FMC}\)(hai góc đối đỉnh)
Do đó: ΔEMB=ΔFMC
=>EM=FM
=>M là trung điểm của EF
BC
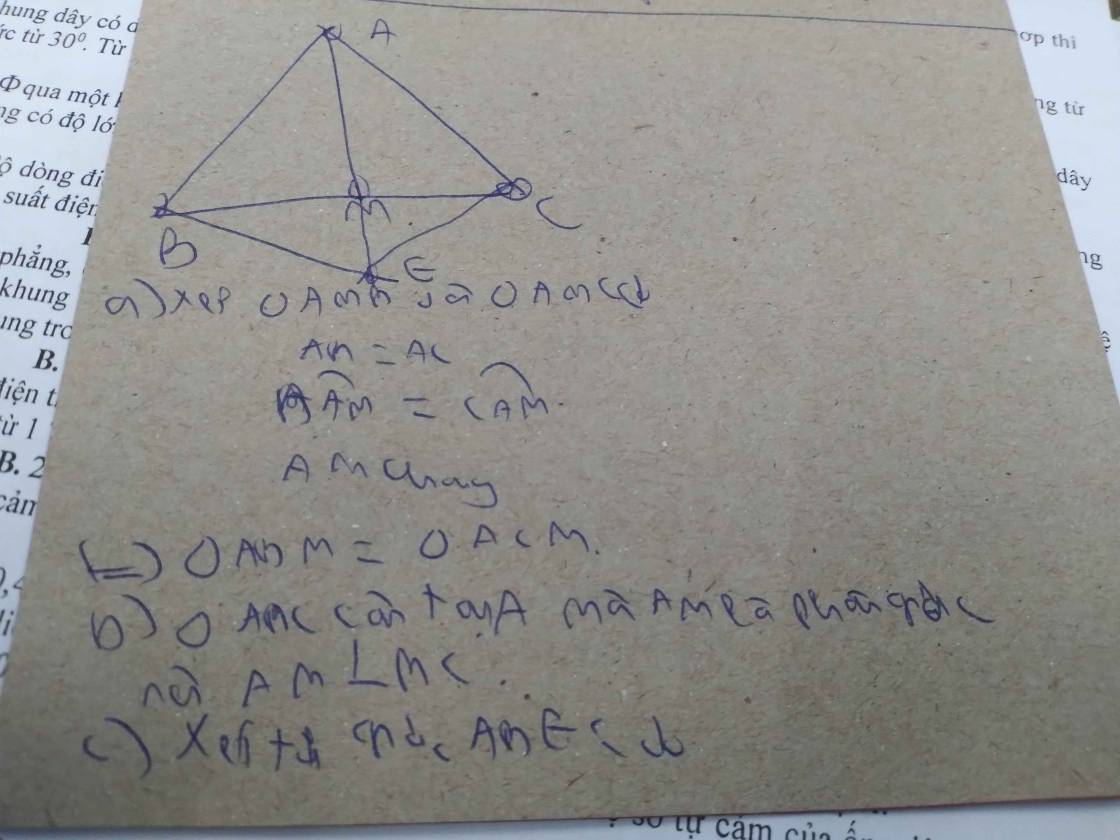
a) Xét \(\Delta AMBva\Delta AMC\) có
\(\hept{\begin{cases}AB=AC\left(gt\right)\\chungAM\\\widehat{BAM}=\widehat{MAC}\left(gt\right)\end{cases}\Rightarrow\Delta ABM=\Delta ACM\left(c-g-c\right)\left(ĐPCM\right)}\)
b) từ 2 tam giác trên = nhau =>BM=CM
xét tam giác BAM và tam giác CEM có
\(\hept{\begin{cases}BM=CM\left(cmt\right)\\AM=ME\left(gt\right)\\\widehat{BMA}=\widehat{EMC}\left(đoi-đinh\right)\end{cases}}\Rightarrow\Delta AMB=\Delta EMC\left(c-g-c\right)\Rightarrow\widehat{BAM}=\widehat{MEC}\left(ĐPCM\right)\)
c) từ hai góc trên = nhau, mà 2 góc đó ở vị trí so le trong =>AB//CE => AK vuông góc với CE => tam giác ACK vuông tại K