cho đường tròn \(\left(O;R\right)\)và đường thẳng \(\left(\Delta\right)\)Ko có điểm chung với đường tròn \(\left(O\right)\), \(H\)là hình chiếu vuông góc của \(O\)trên \(\left(\Delta\right)\). Từ điểm \(M\)bất kì trên \(\left(\Delta\right)\)\(\left(M\ne H\right)\), vẽ 2 tiếp tuyến \(MA\)và \(MB\)tới đường tròn \(\left(O\right)\)( \(A,B\)là các tiếp điểm). Gọi \(K,I\)thứ tự là giao điểm của \(AB\)với \(OM,OH\)
a) CM \(AB=2AK\)và 5 điểm \(M,A,O,B,H\)cùng \(\in\)đường tròn
b) CM \(OI.OH=OK.OM=R^2\)
c) trên đoạn \(OA\)lấy điểm \(N\)sao cho \(AN=2ON\). Đường trung trực của \(BN\)cắt \(OM\)ở \(E\). Tinh tỷ số \(\frac{OE}{OM}\)
P/S: mình làm được câu a, b rồi. CHỉ xin hướng dẫn câu c) thôi ạ


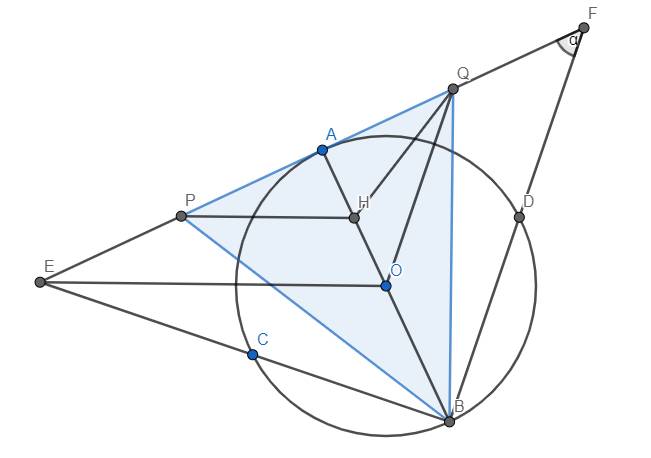

Đường tròn c: Đường tròn qua B_1 với tâm O Đoạn thẳng j: Đoạn thẳng [A, B] Đoạn thẳng k: Đoạn thẳng [O, M] Đoạn thẳng l: Đoạn thẳng [M, H] Đoạn thẳng m: Đoạn thẳng [H, O] Đoạn thẳng n: Đoạn thẳng [A, M] Đoạn thẳng p: Đoạn thẳng [M, B] Đoạn thẳng q: Đoạn thẳng [A, O] Đoạn thẳng r: Đoạn thẳng [O, B] Đoạn thẳng t: Đoạn thẳng [N, B] Đoạn thẳng b: Đoạn thẳng [E, J_1] Đoạn thẳng e: Đoạn thẳng [N, E] Đoạn thẳng f_1: Đoạn thẳng [E, B] Đoạn thẳng g_1: Đoạn thẳng [A, E] O = (6.36, -0.08) O = (6.36, -0.08) O = (6.36, -0.08) Điểm M: Điểm trên f Điểm M: Điểm trên f Điểm M: Điểm trên f Điểm H: Giao điểm đường của f, g Điểm H: Giao điểm đường của f, g Điểm H: Giao điểm đường của f, g Điểm A: Giao điểm đường của c, h Điểm A: Giao điểm đường của c, h Điểm A: Giao điểm đường của c, h Điểm B: Giao điểm đường của c, i Điểm B: Giao điểm đường của c, i Điểm B: Giao điểm đường của c, i Điểm I: Giao điểm đường của g, j Điểm I: Giao điểm đường của g, j Điểm I: Giao điểm đường của g, j Điểm K: Giao điểm đường của j, k Điểm K: Giao điểm đường của j, k Điểm K: Giao điểm đường của j, k Điểm N: A đối xứng qua F Điểm N: A đối xứng qua F Điểm N: A đối xứng qua F Điểm E: Giao điểm đường của a, k Điểm E: Giao điểm đường của a, k Điểm E: Giao điểm đường của a, k Điểm J: Trung điểm của A, N Điểm J: Trung điểm của A, N Điểm J: Trung điểm của A, N
a) Theo tính chất hai tiếp tuyến cắt nhau, ta có tam giác MAB cân tại M có MK là phân giác nên đồng thời là đường trung tuyến. Vậy thì K là trung điểm AB hay \(AK=\frac{AB}{2}\)
Ta thấy các tam giác MHO, MAO, MBO đều là các tam giác vuông chung cạnh huyền MO nên M, H, A, O B cùng thuộc đường tròn đường kính MO.
b) Do K là trung điểm AB nên theo tính chất đường kính dây cung, ta có \(\widehat{IKO}=90^o\)
Suy ra \(\Delta IKO\sim\Delta MHO\left(g-g\right)\Rightarrow\frac{OI}{OM}=\frac{OK}{OH}\Rightarrow OI.OH=OM.OK\)
Xét tam giác vuông MBO, đường cao BK, ta có: \(OK.OM=OB^2=R^2\)
Vậy nên \(OI.OH=OK.OM=R^2\)
c) Ta thấy do trung điểm của BN cắt OM tại E nên EN = EB
Lại có EB = EA vì OM là đường trung trực của AB
Suy ra EA = EN hay tam giác EAN cân tại E.
Gọi J là trung điểm AN.
Xét tam giác cân EAN có EJ là trung tuyến nên đồng thời là đường cao.
Vậy thì \(EJ\perp OA\) hay EJ // AM.
Xét tam giác OAM, áp dụng định lý Talet ta có:
\(\frac{OE}{OM}=\frac{OF}{OA}=\frac{2}{3}\)