Cho biểu thức M = 3 + 3^2 + 3^3 + ... + 3^2009. Tìm số tự nhiên n biết: 2M = 3^n - 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1. Ta có:
3A = 3^2 + 3^3+3^4+...+3^101
=> 3A-A= (3^2+3^3+3^4+...+3^101) - (3+3^2+3^3+...+3^100)
<=> 2A= 3^101-3
=> 2A +3 = 3^101
Mà 2A+3=3^n
=> 3^101 = 3^n => n=101
2. M=3+32+33+34+...+3100
=>3M=32+33+34+35+...+3101
=>3M-M= 3101-3 ( chỗ này bạn tự làm được nhé)
=> M=\(\frac{3^{101}-3}{2}\)
a) Ta co : 3101=(34)25 .3=8125.3
Bạn học đồng dư thức rồi thì xem:
Vì 81 đồng dư với 1 (mod 8) => 8125 đồng dư với 1 (mod 8)=> 8125.3 đồng dư với 1.3=3(mod 8)
=> 8125.3-3 đồng dư với 3-3=0 (mod 8)=> 8125.3-3 chia hết cho 8
=>\(\frac{81^{25}.3-3}{2}\)chia hết cho 4=> M chia hết cho 4 (1)
Ma M=3101-3 chia hết cho 3 (2)
Từ (1) và (2) => M chia hết cho 12
b)\(2\left(\frac{3^{101}-3}{2}\right)+3=3^n\)
=> 3101-3 +3 =3n
=> 3101=3n=> n = 101

Chọn đáp án C.
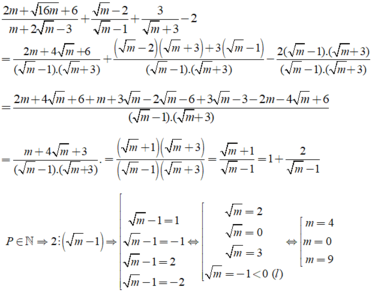
Thử lại, với m= 4 thì P =3 ( thỏa mãn)
Với m = 0 thì P = -1 ( không là số tự nhiên).
Với m = 9 thì P = 2 ( thỏa mãn)
Vậy m = 4 hoặc m = 9.

M = 1 + 3 + 3² + ... + 3²⁰²¹
⇒ 3M = 3 + 3² + 3³ + ... + 3²⁰²²
⇒ 2M = 3M - M
= (3 + 3² + 3³ + ... + 3²⁰²²) - (1 + 3 + 3² + ... + 3²⁰²¹)
= 3²⁰²² - 1
⇒ 2M + 1 = 3²⁰²² + 1 - 1 = 3²⁰²²
Mà 2M + 1 = 3²
⇒ 3²⁰²² = 3²ⁿ
⇒ 2n = 2022
⇒ n = 2022 : 2
⇒ n = 1011
M = 1 + 3 + 32 + ... + 32021
3M = 3(1 + 3 + 32 + ... + 32021)
3M = 3 + 32 + ... + 32022
3M - M = (3 + 32 + ... + 32022) - (1 + 3 + 32 + ... + 32021)
2M = 32022 - 1 (1)
Thay (1) vào 2M + 1 = 3^2N, ta có
2M + 1 = 3^2n
=> 32022 - 1+ 1 = 3^2n
=> 32022 = 3^2n
=> 2n = 2022
=> n = 1011
Vậy n = 1011

=>3A=32+33+…+32010
=>3A-A=32+33+…+32010-3-32-…-32009
=>2A=32010-3
=>2A+3=32010=3N
=>N=2010
A = 3+32+33+......+32009
3A = 32+33+34+......+32010
2A = 3A - A = 32010-3
=> 2A + 3 = 32010
Mà 2A + 3 = 3n
=> n = 2010
Cho biểu thức M mà lại biết 2A. Câu này mới