Cho A= 3+32 +3^3+...+.3^23+3^24, chứng minh A chia hết cho 12
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KV
23 tháng 12 2023
A = 8⁸ + 2²⁰
= (2³)⁸ + 2²⁰
= 2²⁴ + 2²⁰
= 2²⁰.(2⁴ + 1)
= 2²⁰.17 ⋮ 17
Vậy A ⋮ 17
AH
Akai Haruma
Giáo viên
31 tháng 12 2023
Câu 1:
$A=(2+2^2)+(2^3+2^4)+(2^5+2^6)+....+(2^{2019}+2^{2020})$
$=2(1+2)+2^3(1+2)+2^5(1+2)+....+2^{2019}(1+2)$
$=(1+2)(2+2^3+2^5+...+2^{2019})=3(2+2^3+2^5+...+2^{2019})\vdots 3$
-----------------
$A=2+(2^2+2^3+2^4)+(2^5+2^6+2^7)+....+(2^{2018}+2^{2019}+2^{2020})$
$=2+2^2(1+2+2^2)+2^5(1+2+2^2)+....+2^{2018}(1+2+2^2)$
$=2+(1+2+2^2)(2^2+2^5+....+2^{2018})$
$=2+7(2^2+2^5+...+2^{2018})$
$\Rightarrow A$ chia $7$ dư $2$.
AH
Akai Haruma
Giáo viên
31 tháng 12 2023
Câu 2:
$B=(3+3^2)+(3^3+3^4)+....+(3^{2021}+3^{2022})$
$=3(1+3)+3^3(1+3)+...+3^{2021}(1+3)$
$=(1+3)(3+3^3+...+3^{2021})=4(3+3^3+....+3^{2021})\vdots 4$
-------------------
$B=(3+3^2+3^3)+(3^4+3^5+3^6)+...+(3^{2020}+3^{2021}+3^{2022})$
$=3(1+3+3^2)+3^4(1+3+3^2)+....+3^{2020}(1+3+3^2)$
$=(1+3+3^2)(3+3^4+...+3^{2020})=13(3+3^4+...+3^{2020})\vdots 13$ (đpcm)
13 tháng 11 2023
1: \(A=2+2^2+2^3+2^4+...+2^{97}+2^{98}+2^{99}+2^{100}\)
\(=2\left(1+2+2^2+2^3\right)+...+2^{97}\left(1+2+2^2+2^3\right)\)
\(=15\left(2+2^5+...+2^{97}\right)\)
\(=30\left(1+2^4+...+2^{96}\right)⋮30\)
2:
\(B=3+3^2+3^3+...+3^{2022}\)
\(=\left(3+3^2\right)+\left(3^3+3^4\right)+...+\left(3^{2021}+3^{2022}\right)\)
\(=\left(3+3^2\right)+3^2\left(3+3^2\right)+...+3^{2020}\left(3+3^2\right)\)
\(=12\left(1+3^2+...+3^{2020}\right)⋮12\)
ML
1
28 tháng 12 2017
3 + 32 + 33 + ..... + 323 + 324
=) ( 3 + 32 ) + ( 33 + 34 ) + ..... + ( 323 + 324 )
=) ( 3 + 32 ) + 32( 3 + 32 ) + ..... + 322( 3 + 32 )
=) 12 + 32 x 12 + ..... + 322 x 12
=) 12 x ( 32 + ..... + 322 ) chia hết cho 12
Vậy A chia hết cho 12
13 tháng 11 2021
A=2+22+23+...+299+2100A=2+22+23+...+299+2100
⇒2A=22+23+24+...+2100+2101⇒2A=22+23+24+...+2100+2101
⇒A=2101−2⇒A=2101−2
B=3+32+33+...+399+3100B=3+32+33+...+399+3100
⇒3B=32+33+34+...+3100+3101⇒3B=32+33+34+...+3100+3101
⇒2B=3101−3⇒2B=3101−3
⇒B=3101−32
NT
0
12 tháng 12 2021
Bài 1:
\(a,A=\left(2+2^2\right)+\left(2^3+2^4\right)+...+\left(2^{2009}+2^{2010}\right)\\ A=\left(1+2\right)\left(2+2^3+...+2^{2009}\right)=3\left(2+...+2^{2009}\right)⋮3\\ A=\left(2+2^2+2^3\right)+...+\left(2^{2008}+2^{2009}+2^{2010}\right)\\ A=\left(1+2+2^2\right)\left(2+...+2^{2008}\right)=7\left(2+...+2^{2008}\right)⋮7\)
\(b,\left(\text{sửa lại đề}\right)B=\left(3+3^2\right)+\left(3^3+3^4\right)+...+\left(3^{2009}+3^{2010}\right)\\ B=\left(1+3\right)\left(3+3^3+...+3^{2009}\right)=4\left(3+3^3+...+3^{2009}\right)⋮4\\ B=\left(3+3^2+3^3\right)+...+\left(3^{2008}+3^{2009}+3^{2010}\right)\\ B=\left(1+3+3^2\right)\left(3+...+3^{2008}\right)=13\left(3+...+3^{2008}\right)⋮13\)
12 tháng 12 2021
Bài 2:
\(a,\Rightarrow2A=2+2^2+...+2^{2012}\\ \Rightarrow2A-A=2+2^2+...+2^{2012}-1-2-2^2-...-2^{2011}\\ \Rightarrow A=2^{2012}-1>2^{2011}-1=B\\ b,A=\left(2020-1\right)\left(2020+1\right)=2020^2-2020+2020-1=2020^2-1< B\)
E
19 tháng 3 2021
Ta có :
\(A=2+2^2+2^3+2^4...2^{2010}\)\(^0\)
\(=2\left(1+2\right)+2^3\left(1+2\right)+...+2^{2009}\left(1+2\right)\)
\(=2.3+2^3.3+....+2^{2009}.3\)
\(=3\left(2+2^3+....+2^{2009}\right)⋮3\)
Ta có :
\(2+2^2+2^3+2^4+....+2^{2010}\)
\(=2\left(1+2+2^2\right)+2^4\left(1+2+2^2\right)+...+2^{2008}\left(1+2+2^2\right)\)
\(=2.7+2^4.7+....+2^{2008}.7\)
\(=7\left(2+2^4+....+2^{2008}\right)⋮7\)
Vậy \(2^1+2^2+2^3+2^4+...+2^{2010}⋮3\) và \(7\)
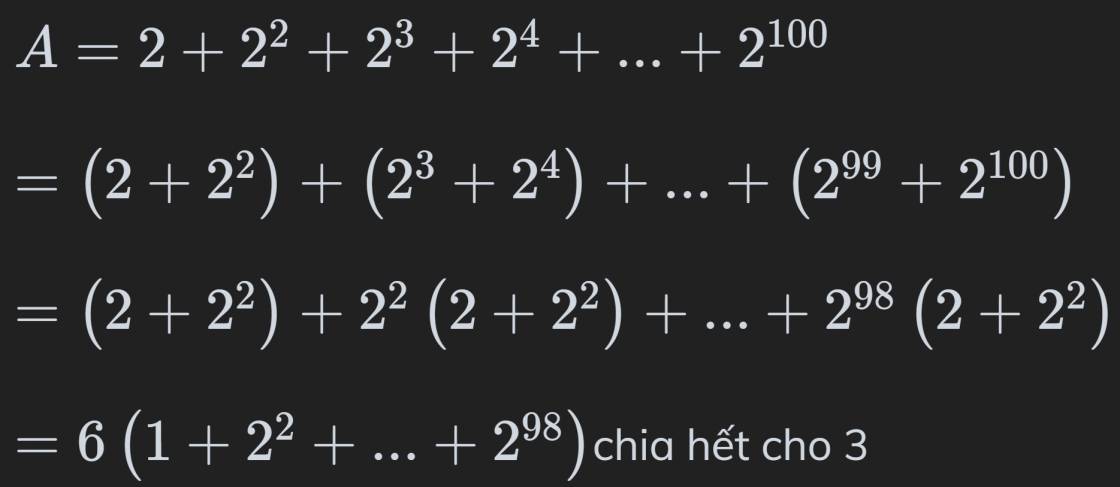
A=3+32 +33+........+324 chia hết cho 13 mới đúng chứ chia hết cho 12 mk ko bít làm
A=(3+32+33)+(34+35+36)+.....+(322+323+324)
A=3(1+3+32)+34(1+3+32)+......+322(1+3+32)
A=(1+3+32)(3+34+....+322)
A=13(3+34+....+322)
=> A chia hết cho 13