Tìm x thuộc tập hợp Z để x + x2 luôn nhận giá trị dương.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
Y
1
TM
22 tháng 7 2015
\(x^2\ge0\)
\(\Rightarrow\)x2+x>0 thì x>0
Vậy x2+x>0 thì x>0
*****nhiều nha
VM
1
AH
Akai Haruma
Giáo viên
15 tháng 10 2021
Lời giải:
Để $\frac{2}{A}$ dương thì $A$ dương
$\Leftrightarrow \sqrt{x}>1 \Leftrightarrow x>1$
\(\frac{2}{A}=\frac{2(\sqrt{x}+1)}{\sqrt{x}-1}=\frac{2(\sqrt{x}-1)+4}{\sqrt{x}-1}=2+\frac{4}{\sqrt{x}-1}\)
Để $A$ nhận giá trị nguyên dương lớn nhất thì $\sqrt{x}-1$ phải nhận giá trị nguyên dương nhỏ nhất.
Với $x>1$ thì $\sqrt{x}-1$ nguyên dương nhỏ nhất bằng $1$
$\Lefrightarrow \sqrt{x}=2$
$\Leftrightarrow x=4$
Vậy $x=4$ thì $\frac{2}{A}$ nhận giá trị nguyên dương lớn nhất.
CM
30 tháng 1 2018
{x ∈Z | - 5 ≤ x ≤ 5 } ⇒ x ∈ {-5; -4; -3; -2; -1; 0; 1; 2; 3; 4; 5}
Phương trình (1) có nghiệm là x = 3 và x = 5.
Phương trình (2) có nghiệm là x = 0.
Phương trình (3) không có nghiệm.
PN
8 tháng 5 2016
a)Ta có ; để A thuộc N <=> (2n+5) chia hết cho (3n+1)
<=> 3(2n+5) chia hết cho (3n+1)
<=>(6n+15) chia hết cho (3n+1)
<=> (6n + 2 +13) chia hết cho (3n+1)
<=> 13 chia hết cho (3n+1)
=> (3n+1) thuộc Ư(13)
Vì n thuộc N
=> (3n+1) = 1,13
=> n = 0 hoặc 4
b)Trong phần này ta sẽ áp dung 1 tính chất sau:
a/b < (a+m)/(b+m) với a<b
Ta thấy :
x/(x+y) > x/(x+y+z)
y/(y+z) > y/(x+y+z)
z/(z+x) > z/(x+y+z)
=> A > x/(x+Y+z) + y/(x+y+z) + z/(x+y+z)
=> A>1
Ta thấy :
x/x+y < (x+z)/(x+y+z)
y/y+z < (y+x)/(x+y+z)
z/z+x < (z+y)/(x+y+z)
=> A < (x+z)/(x+y+z) +(y+x)/(x+y+z) +(z+y)/(x+y+z)
=>A< 2(x+y+z)/(x+y+z)
=> A<2
=>1<A<2
=> A ko phải là số nguyên(đpcm)
DT
25 tháng 7 2016
\(1.\frac{x-7}{2}< 0\)
\(\Leftrightarrow\frac{x-7}{2}.2< 0.2\)
\(\Leftrightarrow x-7< 0\Leftrightarrow x< 7\)
\(S=\left\{xlx< 7\right\}\)
2)\(\)Đề biểu thức sau nhân giá trị âm thì :
\(\frac{x+3}{x-5}< 0\Leftrightarrow x+3< 0\Leftrightarrow x< 3\left(Đk:x\ne5\right)\)
\(S=\left\{xlx< 3\right\}\)
3.Giá trị của x thuộc Z để biểu thức sau nhận giá trị dương:
\(x^2+x\ge0\)
\(\Leftrightarrow x\left(x+1\right)\ge0\)
\(\Leftrightarrow\orbr{\begin{cases}x\ge0\\x+1\ge0\end{cases}\Leftrightarrow\orbr{\begin{cases}x\ge0\\x\ge-1\end{cases}}}\)
\(S=\left\{xlx\ge-1\right\}\)
21 tháng 12 2021
a: \(M=\dfrac{x^2-3x+2x^2+6x-3x^2-9}{\left(x-3\right)\left(x+3\right)}=\dfrac{3}{x+3}\)
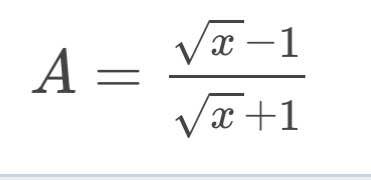
x^2 + x = x^2 + 2x.1/2 + 1/4 - 1/4 \
nhớ chọn mình nha!!!!!!!!!!!!!!!!!!!!!