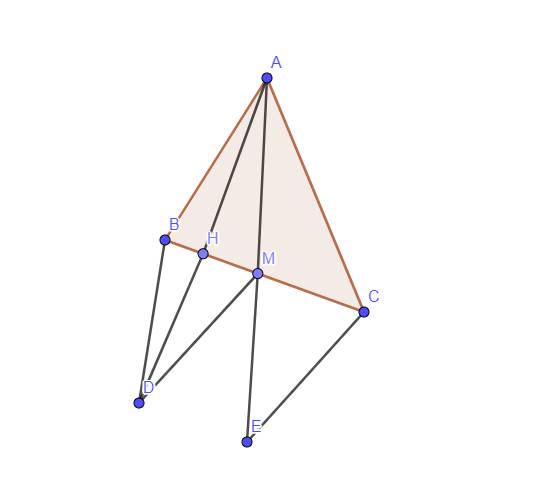
Cho tam giác ABC.Gọi M là trung điểm của cạnh BC.Trên tia AM lấy điểm D sao cho AM=MD
a)Chứng minh:tam giác AMB=tam giác DMC
b)Vẽ AH vuông góc với BC tại H.Trên tia đối của tia HA lấy điểm E sao cho HE=HA.Chứng minh:ME=MD
c)Chứng minh :góc MED-góc MDE.Chứng minh DE song song BC
(ko cần vẽ hình các bn nhé!!!)