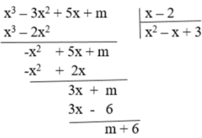Tìm m sao cho đa thức 2x3 +3x2 - 5x + 2 chia cho đa thức 2x + m dư 5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
23 tháng 12 2021
Đặt \(f\left(x\right)=2x^3-3x^2+x+a\)
Ta có: phép chia \(f\left(x\right)\) cho \(x+2\) có dư là \(R=f\left(-2\right)\)
\(\Rightarrow f\left(-2\right)=2.\left(-2\right)^3-3.\left(-2\right)^2+\left(-2\right)+a\)
\(f\left(-2\right)=2.\left(-8\right)-3.4-2+a\)
\(f\left(-2\right)=-16-12-2+a\)
\(f\left(-2\right)=-20+a\)
Để \(f\left(x\right)\) chia hết cho \(x+2\) thì \(R=0\) hay \(f\left(-2\right)=0\)
\(\Rightarrow-20+a=0\Leftrightarrow a=20\)
AH
Akai Haruma
Giáo viên
8 tháng 5 2022
Lời giải:
a.
\(C(x)=A(x)+B(x)=(2x^3-3x^2-x+1)+(-2x^3+3x^2+5x-2)\)
\(=(2x^3-2x^3)+(-3x^2+3x^2)+(-x+5x)+(1-2)=4x-1\)
b.
$C(x)=4x-1=0$
$\Rightarrow x=\frac{1}{4}$
Vậy $x=\frac{1}{4}$ là nghiệm của $C(x)$
c.
\(D(x)=A(x)-B(x)=(2x^3-3x^2-x+1)-(-2x^3+3x^2+5x-2)\)
\(=2x^3-3x^2-x+1+2x^3-3x^2-5x+2\)
\(=4x^3-6x^2-6x+3\)
AH
Akai Haruma
Giáo viên
15 tháng 9 2021
Lời giải:
a. $f(x)=x^4-3x^2+2x-7=x^3(x+2)-2x^2(x+2)+x(x+2)-7$
$=(x+2)(x^3-2x^2+x)-7=g(x)(x^3-2x^2+x)-7$
Vậy $f(x)$ chia $g(x)$ được thương là $x^3-2x^2+x$ và dư là $-7$
b. Theo phần a $f(x)=(x^3-2x^2+x)g(x)-7$
Với $x$ nguyên, để $f(x)\vdots g(x)$ thì $7\vdots g(x)$
$\Leftrightarrow x+2$ là ước của $7$
$\Rightarrow x+2\in\left\{\pm 1;\pm 7\right\}$
$\Leftrightarrow x\in\left\{-3; -1; 5; -9\right\}$
c.
Theo định lý Bezout về phép chia đa thức, để $K(x)=-2x^3+x-m\vdots x+2$ thì: $K(-2)=0$
$\Leftrightarrow -2(-2)^3+(-2)-m=0$
$\Leftrightarrow 14-m=0$
$\Leftrightarrow m=14$
LM
7
27 tháng 12 2018
Để \(2x^3-5x^2+6x+m⋮2x-5\) thì :
\(2x^3-5x^2+6x+m=\left(2x-5\right)\cdot Q\)
Đặt \(x=\frac{5}{2}\)ta có :
\(2\left(\frac{5}{2}\right)^3-5\left(\frac{5}{2}\right)^2+6\cdot\frac{5}{2}+m=\left(2\cdot\frac{5}{2}-5\right)\cdot Q\)
\(15+m=0\)
\(m=-15\)
Vậy........
T
27 tháng 12 2018
Bài làm chỉ mang t/c tham khảo,chưa biết đúng hay sai.
Ta có: \(\frac{2x^3-5x^2+6x+m}{2x-5}=\frac{2x^3-5x^2+2x-5+4x+5+m}{2x-5}\)
\(=1+\frac{2x^3-5x^2+4x+5+m}{2x-5}=1+\frac{2x^3-5x^2+2x-5+2x+10+m}{2x-5}\)
\(=2+\frac{2x^3-5x^2+2x+10+m}{2x-5}=3+\frac{2x^3-5x^2+15+m}{2x-5}\)
\(=104+\frac{1}{15}m\).
Để \(2x^3-5x^2+6x+m⋮2x-5\) thì \(\frac{1}{15}m\) là số nguyên hay \(\frac{m}{15}\) nguyên hay \(m\in B\left(15\right)\)
25 tháng 9 2021
1) \(\Leftrightarrow\left(x-4\right)\left(x+4\right)-x\left(x-4\right)=0\)
\(\Leftrightarrow\left(x-4\right)\left(x+4-x\right)=0\)
\(\Leftrightarrow\left(x-4\right)4=0\)
\(\Leftrightarrow x=4\)
2) \(\left(x+3\right)^2-\left(x-3\right)\left(x+5\right)=x^2+6x+9-x^2-2x+15=4x+24\)
3) \(2x^3+3x^2-2x+a=2x^2\left(x-2\right)+7x\left(x-2\right)+16\left(x-2\right)+32+a\)
Để \(2x^3+3x^2-2x+a⋮x-2\) thì \(32+a=0\Leftrightarrow a=-32\)
HP
25 tháng 9 2021
1.
x2 - 16 - x(x - 4) = 0
<=> (x2 - 42) - x(x - 4) = 0
<=> (x - 4)(x + 4) - x(x - 4) = 0
<=> (x + 4 - x)(x + 4) = 0
<=> 4(x + 4) = 0
<=> x + 4 = 0
<=> x = -4
2.
(x + 3)2 - (x - 3)(x + 5)
= x2 + 6x + 9 - (x2 + 5x - 3x - 15)
= x2 + 6x + 9 - x2 + 5x - 3x - 15
= x2 - x2 + 6x + 5x - 3x + 9 - 15
= 8x - 6
M
1
5 tháng 11 2021
\(\Leftrightarrow2x^3+x-a=\left(2x-5\right)\cdot a\left(x\right)\)
Thay \(x=\dfrac{5}{2}\Leftrightarrow2\cdot\dfrac{125}{8}+\dfrac{5}{2}-a=0\Leftrightarrow a=\dfrac{135}{4}\)
PT
1
CM
24 tháng 2 2018
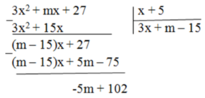
A(x) chia cho B(x) có số dư bằng 2 nên 102 – 5m = 2 ⇒ -5m = 100
⇒ m = 20