Cho đường tròn (O) .BC là dây bất kì (BC=a (const)). Trên cung lớn BC lấy điểm A. H là trực tâm của tam giác ABC. K là chân đường cao kẻ từ A. Tìm giá trị lớn nhất của tích AH.AK
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Vẽ các đường kính AM, BN, CP của (O). Dễ cm được BMCH, CNAH,APBH là các hình bình hành => AH = CN; BH = CM; CH = BM
=> AH + BH + CH = CN + CM + BM
Vì BC cố định nên CN không đổi => (AH + BH + CH) max khi (CM + BM) max. Ta sẽ cm rằng điều đó xảy ra khi M trùng điểm chính giữa cung nhỏ BC.
Thật vậy gọi Q là điểm chính giữa cung nhỏ BC. Kéo dài BQ đoạn QD = BQ = CQ, kéo dài BM đoạn ME = MC => BD = BQ + CQ = 2BQ và BE = BM + CM
Vì tg CQD cân tại Q => ^BDC = ^QCD = ^BQC/2
Tương tự tg CME cân tại M => ^BEC = ^MCE = ^BMC/2
Mà ^BMC = ^BQC => ^BEC = ^BDC => B,C,D,E cùng thuộc đường tròn đường kính BD => BE =< BD <=> BM + CM =< 2BQ => (BM + CM)
Max = 2BQ xảy ra khi E trùng D hay khi M trùng Q khi đó A là điểm chính giữa cung lớn BC

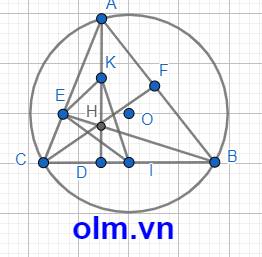
a, Xét tam giác vuông EBC vuông tại E và CI = IB
⇒ IE = IC = IB (1) ( vì trong tam giác vuông trung tuyến ứng với cạnh huyền bằng \(\dfrac{1}{2}\) cạnh huyền)
Xét tam giác vuông BCF vuông tại F và IC =IB
⇒IF = IC = IB (2) (vì trong tam giác vuông trung tuyến ứng với cạnh huyền bằng \(\dfrac{1}{2}\) cạnh huyền)
Từ (1) và (2) ta có:
IE = IF = IB = IC
Vậy bốn điểm B, C, E, F cùng thuộc một đường tròn tâm I bán kính bằng \(\dfrac{1}{2}\) BC (đpcm)
b, Xét \(\Delta\)AFC và \(\Delta\)AEB có:
\(\widehat{CAF}\) chung ; \(\widehat{AFC}\) = \(\widehat{AEB}\) = 900
⇒ \(\Delta\)AFC \(\sim\) \(\Delta\)AEB (g-g)
⇒ \(\dfrac{AF}{AE}\) = \(\dfrac{AC}{AB}\) (theo định nghĩa hai tam giác đồng dạng)
⇒AB.AF = AC.AE (đpcm)
Xét tam giác vuông AEH vuông tại E và KA = KH
⇒ KE = KH ( vì trong tam giác vuông trung tuyến ứng với cạnh huyền bằng \(\dfrac{1}{2}\) cạnh huyền)
⇒\(\Delta\)EKH cân tại K ⇒ \(\widehat{KEH}\) = \(\widehat{EHK}\)
\(\widehat{EHK}\) = \(\widehat{DHB}\) (vì hai góc đối đỉnh)
⇒ \(\widehat{KEH}\) = \(\widehat{DHB}\) ( tc bắc cầu) (3)
Theo (1) ta có: IE = IB ⇒ \(\Delta\) IEB cân tại I
⇒ \(\widehat{IEB}\) = \(\widehat{IBE}\) (4)
Cộng vế với vế của (3) và(4)
Ta có: \(\widehat{KEI}\) = \(\widehat{KEH}\) + \(\widehat{IEB}\) = \(\widehat{DHB}\) + \(\widehat{IBE}\) = \(\widehat{DHB}\) + \(\widehat{DBH}\)
Vì tam giác DHB vuông tại D nên \(\widehat{DHB}\) + \(\widehat{DBH}\) = 1800 - 900 = 900
⇒\(\widehat{KEI}\) = 900
IE \(\perp\) KE (đpcm)

a: Kẻ BD vuông góc AC,CE vuông góc AB
góc BEC=góc BDC=90 độ
=>BEDC nội tiếp
=>góc AED=góc ACB
=>ΔAED đồng dạng vơi ΔACB
Tâm M của đường tròn ngoại tiếp tứ giác BDCE là trung điểm của BC
Gọi H là giao của BD và CE
=>AH vuông góc BC tại N
Gọi giao của OM với (O) là A'
ΔOBC cân tại O
=>OM vuông góc BC
AN<=A'M ko đổi
=>\(S_{ABC}=\dfrac{1}{2}\cdot AN\cdot BC< =\dfrac{1}{2}\cdot A'M\cdot BC_{kođổi}\)
Dấu = xảy ra khi A trùng A'
=>A là điểm chính giữa của cung BC
Gọi bán kính đường tròn là R.
Kẻ đường kính CO cắt đường tròn (O) tại J. Gọi I là chân đường vuông góc hạ từ O đến BC. Theo tính chất đường kính dây cung : I là trung điểm BC.
Do độ lớn BC không đổi nên OI cũng không đổi. Ta tính được \(OI=\sqrt{R^2-\frac{a^2}{4}}\)
Do JC là đường kính nên \(\widehat{JAC}=\widehat{JBC}=90^o\)
Suy ra JA // BH; JB // AH.
Vậy tứ giác JAHB là hình bình hành. Ta có AH = JB.
Xét tam giác JBC có O là trung điểm JC, I là trung điểm BC nên OI là đường trung bình.
Vậy thì JB = 2OI.
Từ đó suy ra AH = 2 OI = \(2\sqrt{R^2-\frac{a^2}{4}}\) (const)
Vậy thì \(AH.AK=2\sqrt{R^2-\frac{a^2}{4}}.AK\)
AK lớn nhất khi A là điểm chính giữa cung BC.
Khi đó \(AK\equiv AI=3OI=3\sqrt{R^2-\frac{a^2}{4}}\)
Vậy thì maxAH.AK \(=2\sqrt{R^2-\frac{a^2}{4}}.3\sqrt{R^2-\frac{a^2}{4}}=6\left(R^2-\frac{a^2}{4}\right)\)