Cho \(\Delta ABC=\Delta DÈF\). Tính chu vi mỗi \(\Delta\), biết ràng AB = 5cm, BC = 7cm, DF = 6 cm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


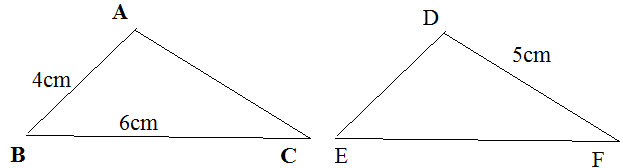
Vì \(\Delta ABC=\Delta DEF\)
nên AB = DE = 4cm;
BC = EF = 6cm;
AC = DF = 5cm
Khi đó: \(P_{\Delta ABC}=P_{\Delta DEF}=4+5+6=15\left(cm\right)\)
Vậy \(P_{\Delta ABC}=P_{\Delta DEF}=15cm.\)

Hình vẽ
Vì ΔABC = ΔDEF nên suy ra:
AB = DE = 4cm
BC = EF = 6cm
DF = AC = 5cm
Chu vi tam giác ABC bằng:
AB + BC + CA = 4 + 6 + 5 = 15 (cm)
Chu vi tam giác DEF bằng:
DE + EF + DF = 4 + 6 + 5 = 15 (cm)
Vậy...
Chúc bạn học tốt!

Bài 2 :
A B D C M K F
a) Xét \(\Delta ABM,\Delta ADM\) có :
\(AB=AD\left(gt\right)\)
\(AM:chung\)
\(BM=DM\) (M là trung điểm của BD)
=> \(\Delta ABM=\Delta ADM\left(c.c.c\right)\)
b) Từ \(\Delta ABM=\Delta ADM\) (cmt - câu a) suy ra :
\(\widehat{AMB}=\widehat{AMD}\) (2 góc tương ứng)
Mà : \(\widehat{AMB}+\widehat{AMD}=180^o\left(Kềbù\right)\)
=> \(\widehat{AMB}=\widehat{AMD}=\dfrac{180^o}{2}=90^o\)
=> \(AM\perp BD\rightarrowđpcm\)
c) Xét \(\Delta ABK,\Delta ADK\) có :
AB = AD (gt)
\(\widehat{BAK}=\widehat{DAK}\) (\(\Delta ABM=\Delta ADM\))
AK :Chung
=> \(\Delta ABK=\Delta ADK\left(c.g.c\right)\)
d) Ta có : \(\left\{{}\begin{matrix}\widehat{ABK}+\widehat{FBK}=180^{^O}\\\widehat{ADK}+\widehat{CDK}=180^{^O}\end{matrix}\right.\left(Kềbù\right)\)
Lại có : \(\widehat{ABK}=\widehat{ADK}\) (do \(\Delta ABK=\Delta ADK\left(c.g.c\right)\)
Nên : \(180^o-\widehat{ABK}=180^o-\widehat{ADK}\)
\(\Leftrightarrow\widehat{FBK}=\widehat{CDK}\)
Xét \(\Delta BFK,\Delta DCK\) có :
\(BF=CD\left(gt\right)\)
\(\widehat{FBK}=\widehat{CDK}\left(cmt\right)\)
\(BK=DK\) (\(\Delta ABK=\Delta ADK\left(c.g.c\right)\))
=> \(\Delta BFK=\Delta DCK\left(c.g.c\right)\)
=> FK = DK (2 cạnh tương ứng)
=> K là trung điểm của FD
=> F, D, K thẳng hàng.

a) Các cạnh còn lại của mỗi tam giác:
-Tam giác ABC: cạnh AC=6cm
-Tam giác DEF:cạnh DE=7cm,cạnh EF=5cm
b)Chu vi của mỗi tam giác đều bằng:18cm

TAM GIÁC ĐỒNG DẠNG
1, a) Tỉ số hai đoạn thẳng AB và AC : \(\frac{AB}{AC}=\frac{6}{15}\)
b) Tỉ số hai đoạn thẳng AB và AC . : \(\frac{AB}{AC}=\frac{6}{18}=\frac{1}{3}\)
2, ΔMNP ~ ΔABC thì : \(\frac{MN}{AB}=\frac{NP}{BC}=\frac{MP}{AC}\)
3, Tìm tam giác đồng dạng có độ dài ba cạnh dưới đây:
A. 4 cm; 5 cm; 6 cm và 4 cm; 5 cm; 7 cm. B. 2 cm; 3 cm; 4 cm và 2 cm ; 5cm ; 4 cm.
C. 6 cm; 5 cm; 7 cm và 6 cm; 5 cm; 8 cm. D. 3 cm; 4 cm; 5cm và 6 cm;8 cm; 10 cm.
4, a) Cho ΔABC có AB=3 cm, AC= 6 cm. Đường phân giác trong của ❏BAC cắt cạnh BC tại E. Biết BD= 2cm. Tính độ dài đoạn thẳng EC ❓
Bạn ơi D ở đâu vậy ?
b) Cho ΔABCΔABC có AB = 6 cm, AC= 8 cm. Đường phân giác trong của ❏BAC cắt cạnh BC tại D. Biết CD= 4 cm. Tính độ dài đoạn thẳng DB ❓
Xét \(\Delta ABC\) có AD là phân giác
\(\Rightarrow\frac{AB}{BD}=\frac{AC}{CD}\Rightarrow BD=\frac{AB.CD}{AC}=3cm\)
5. a) Cho ΔDEF∼ΔABC theo tỉ số đồng dạng k = 2. Tìm tỉ số SDÈFvà SABC
\(\frac{S_{\Delta DEF}}{S_{\Delta ABC}}=k^2=2^2=4\)
b) Cho ΔDEF∼ΔABC theo tỉ số đồng dạng k=\(\frac{1}{2}\). Tìm tỉ số SDEF và SABC
\(\frac{S_{\Delta DEF}}{S_{\Delta ABC}}=k^2=\left(\frac{1}{2}\right)^2=\frac{1}{4}\)
6. Cho ΔABC..Lấy 2 điểm D và E lần lượt nằm trên cạnh AB và AC sao cho AD/AB=AE/AC Kết luận nào sai ❓
A. ΔADE∼ΔABC B. DE//BC
C. AE/AD=AC/AB D. ΔADE=ΔABC
7, Nếu hai tam giác ABC và DEF có góc A= góc D, góc C= góc E thì:
A.ΔABC∼ΔDEF B. ΔABC∼ΔEDF
C. ΔABC∼ΔDFE D.ΔABC∼ΔFED
\(\Delta ABC=\Delta DEF\)
\(\Rightarrow\hept{\begin{cases}AB=DE\text{ ( 2 cạnh tương ứng )}\\BC=EF\text{ ( 2 cạnh tương ứng )}\\AC=DF\text{ ( 2 cạnh tương ứng )}\end{cases}}\)
\(\Rightarrow\)AB = DE = 5cm ; BC = EF = 7cm ; AC = DF = 6cm
\(\Rightarrow\)chu vi \(\Delta ABC\)là : 5 + 7 + 6 = 18 ( cm )
chu vi \(\Delta DEF\)là : 5 + 7 + 6 = 18 ( cm )
Vì tam giác ABC = tam giác DEF
=> AB = DE; BC = EF; AC = DF
Chu vi tam giác ABC là: 5 + 6 + 7 = 18 (cm) = chu vi tam giác DEF
Vậy chu vi tam giác ABC là 18 cm
chu vi tam giác DEF là 18 cm