Cho tam giác ABC vuông tại A ( AB<AC ) đường cao AH . Gọi K là trung điểm của BC , D là điểm đối xứng của A qua K . Tứ giác ABCD là hình gì . gọi M là điểm đối xứng của A qua H , chứng minh tứ giác BCDM là hình thang . Chúng minh tam giác KBM cân
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
BN
5 tháng 4 2022
sửa đề nha
cho tam giác ABC vuông tại A , trên tia đối tia AB lấy đỉnh M sao cho AB=AM a. CMR : tam giác ABC = tam giác AMC
b. kẻ AH vuông góc với BC tại H kẻ AK vuông gói với MC tại K CMR : BH = MK
c. CMR : HK // BM
BN
5 tháng 4 2022
Xét \(\Delta BACvà\Delta MACcó\)
AC:chung
AM=AB(gt)
\(\widehat{MAC}=\widehat{BAC}\)( vì AC⊥BC)
3 tháng 2 2021
a) Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC(ΔABC cân tại A)
AH chung
Do đó: ΔAHB=ΔAHC(cạnh huyền-cạnh góc vuông)
b) Xét ΔDHB vuông tại D và ΔEHC vuông tại E có
HB=HC(ΔAHB=ΔAHC)
\(\widehat{DBH}=\widehat{ECH}\)(hai góc ở đáy của ΔABC cân tại A)
Do đó: ΔDHB=ΔEHC(cạnh huyền-góc nhọn)
nên \(\widehat{DHB}=\widehat{EHC}\)(hai góc tương ứng)
mà \(\widehat{DHB}=\widehat{FHC}\)(hai góc đối đỉnh)
nên \(\widehat{EHC}=\widehat{FHC}\)
mà tia HC nằm giữa hai tia HE,HF
nên HC là tia phân giác của \(\widehat{EHF}\)(đpcm)
5 tháng 3 2021
a) Xét ΔADB vuông tại D và ΔADC vuông tại D có
AB=AC(ΔABC cân tại A)
AD chung
Do đó: ΔADB=ΔADC(cạnh huyền-cạnh góc vuông)
10 tháng 3 2023
`a)`
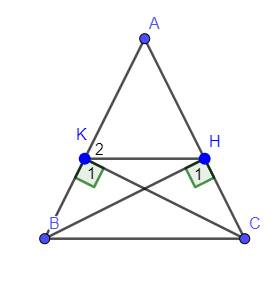
+, Có `Delta ABC` cân tại `A(GT)=>hat(ABC)=hat(ACB)`
hay `hat(KBC)=hat(HCB)`
Xét `Delta BHC` và `Delta CKB` có :
`{:(hat(H_1)=hat(K_1)(=90^0)),(BC-chung),(hat(HCB)=hat(KBC)(cmt)):}}`
`=>Delta BHC=Delta CKB(c.h-g.n)(đpcm)`
+, Có `Delta BHC=Delta CKB(cmt)`
`=>HC=BK` ( 2 cạnh t/ứng )
mà `AB=AC(Delta ABC` cân tại `A)`
nên `AB-BK=AC-CH`
hay `AK=AH`
`=>Delta AHK` cân tại `A(đpcm)`
`b)`
Có `Delta ABC` cân tại `A(GT)=>hat(ABC)=(180^0-hat(A))/2` (1)
`Delta AHK ` cân tại `A(cmt)=>hat(K_2)=(180^0-hat(A))/2` (2)
Từ (1) và (2) suy ra :
`hat(ABC)=hat(K_2)`
mà `2` góc này ở vị trí Đồng vị
nên `KH////BC(đpcm)`
