Giúp mình với mình cần gấp đây Câu 1 : cho đường tròn (o) Đường kính AB điểm M. thuộc đường tròn Vẽ điểm N đối xứng với Aqua M , BN cắt đường tròn ở C gọi e là giao điểm của AC và BM a) CMR : NE vuông góc với AB b) Gọi F là điểm đối xứng với E qua M . CMR : Fa là tiếp tuyến (o). c) FN là tiếp tuyến ( B ; BA)

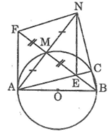
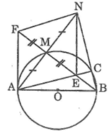
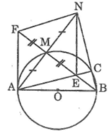

a. Xét tam giác NAB có đường cao AC,BM
mà AC,BM cắt nhau tại E
=> E là trực tâm tam giác NAB
=>NE là đường cao
\(\Rightarrow NE\perp AB\) (đpcm)
b. Vì N là điểm đối xứng với A qua M
=> M là trung điểm của AN
Vì F là điểm đối xứng với E qua M
=> M là trung điểm của EF
=> Tứ giác AFNE là hình bình hành
=> NE//AF
mà \(NE\perp AB\)
\(\Rightarrow AF\perp AB\)
=> AF là tiếp tuyến của (O) (đpcm)
c. Vì tam giác BAN có đường cao BM, đường trung tuyến BM
\(\Rightarrow\Delta BAN\)cân tại B
=> BM là đường phân giác
Xét ΔBAF và ΔBNF có:
BA = BN
BF chung
góc ABF= góc NBF ( vì BF là đường phân giác)
Suy ra : ΔBAF = ΔBNF (c.g.c)
-> góc BAF=góc BNF =900
\(\Rightarrow BN\perp NF\)
=> FN là tiếp tuyến của đường tròn (B,BN) hay đường tròn (B,BA) (đpcm)
a) Tam giác ABM nội tiếp trong đường tròn (O) có AB là đường kính nên vuông tại M
Suy ra: AN ⊥ BM
Tam giác ABC nội tiếp trong đường tròn (O) có AB là đường kính nên vuông tại C
Suy ra: AC ⊥ BN
Tam giác ABN có hai đường cao AC và BM cắt nhau tại E nên E là trọng tâm của tam giác ABN
Suy ra: NE ⊥ AB
b) Ta có: MA = MN ( tính chất đối xứng tâm)
ME = MF ( tính chất đối xứng tâm)
Tứ giác AENF có hai đường chéo cắt nhau tại trung điểm của mỗi điểm đường nên nó là hình bình hành.
Suy ra: AF // NE
Mà NE ⊥ AB ( chứng minh trên)
Suy ra: AF ⊥ AB tại A.
Vậy FA là đường trung tuyến của đường tròn (O).
c) Trong tam giác ABN ta có: AN ⊥ BM và AM = AN
Suy ra tam giác ABN cân tại B.
Suy ra BA = BN hay N thuộc đường tròn (B; BA)
Tứ giác AFNE là hình bình hành nên AE // FN hay FN // AC
Mặt khác: AC ⊥ BN ( chứng minh trên)
Suy ra: FN ⊥ BN tại N
Vậy FN là tiếp tuyến của đường tròn ( B; BA).