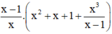Thực hiện phép chia sau theo 2 cách : cách thông thường và cách rút gọn : 432 : 5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NH
1
25 tháng 9 2017
ta có \(27^5:81^3=\left(3^3\right)^5:\left(3^4\right)^3=3^{15}:3^{12}\)
=\(3^{15-12}=3^3=27\)
TV
2
TN
11 tháng 10 2020
Cách 1:
\(\left(\frac{1}{3}+\frac{1}{5}\right):\frac{2}{5}=\frac{8}{15}:\frac{2}{5}=\frac{8}{15}\times\frac{5}{2}=\frac{4}{3}\)
Cách 2:
\(\left(\frac{1}{3}+\frac{1}{5}\right):\frac{2}{5}=\frac{1}{3}:\frac{2}{5}+\frac{1}{5}:\frac{2}{5}=\frac{5}{6}+\frac{1}{2}=\frac{4}{3}\)
Học tốt ah
11 tháng 10 2020
Cách 1:
\(\left(\frac{1}{3}+\frac{1}{5}\right):\frac{2}{5}=\left(\frac{5}{15}+\frac{3}{15}\right)\cdot\frac{5}{2}=\frac{8}{15}\cdot\frac{5}{2}=\frac{40}{30}=\frac{4}{3}\)
Cách 2:
\(\left(\frac{1}{3}+\frac{1}{5}\right):\frac{2}{5}=\left(\frac{1}{3}+\frac{1}{5}\right)\cdot\frac{5}{2}=\frac{1}{3}\cdot\frac{5}{2}+\frac{1}{5}\cdot\frac{5}{2}=\frac{5}{6}+\frac{1}{2}=\frac{5}{6}+\frac{3}{6}=\frac{8}{6}=\frac{4}{3}\)
CM
5 tháng 11 2018
Cách 1:Không áp dụng tính phân phối:
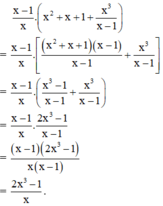
Cách 2: Áp dụng tính chất phân phối: A( B+ C)= AB + AC
AH
Akai Haruma
Giáo viên
26 tháng 12 2022
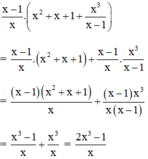
Bài 1:
1.
$A=(x-2)^2+6x+5=x^2-4x+4+6x+5=x^2+2x+9$
2.
$B=\frac{15x^2y^3}{5x^2y^2}-\frac{10x^3y^2}{5x^2y^2}+\frac{5x^2y^2}{5x^2y^2}$
$=3y-2x+1$
AH
Akai Haruma
Giáo viên
26 tháng 12 2022
Bài 3:
$f(x)=x+4x^2-5x+3=4x^2-4x+3=4x(x-3)+8(x-3)+27$
$=(x-3)(4x+8)+27=g(x)(4x+8)+27$
Vậy $f(x):g(x)$ có thương là $4x+8$ và dư là $27$
CM
3 tháng 3 2019
Cách 1:Không áp dụng tính phân phối:
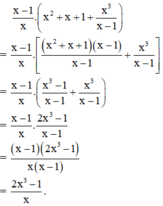
Cách 2: Áp dụng tính chất phân phối: A( B+ C)= AB + AC
23 tháng 8 2017
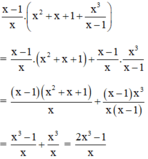
Ta có:\(x\left(x+y\right)+y\left(x-y\right)=x^2+xy+xy-y^2\)
\(=x^2+2xy-y^2\)
\(=-\left(x^2-2xy+y^2\right)+2x^2\)
Áp dụng hằng đẳng thức (a-b)2=a2-2ab+b2 ta đc:
\(=2x^2-\left(x-y\right)^2\)
Tại x = - 8 ; y = 7 ta đc:
\(=2\left(-8\right)^2-\left(-8-7\right)^2\)
\(=-241\)