tìm tất cả các cặp x,y thỏa mãn:
6x+99=20.y
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
6 tháng 10 2017
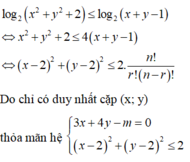
nên đường thẳng 3x + 4y - m = 0 là tiếp tuyến của đường tròn (x – 2)2 + (y – 2)2 = 2.
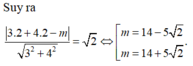
Chọn C.
TQ
0
HN
2
9 tháng 4 2023
\(x.\left(y-1\right)+y=2\)
\(x.\left(y-1\right)+\left(y-1\right)=2-1\)
\(\left(y-1\right)\left(x-1\right)=1\)
(y-1) ; (x-1) có 2 cặp: \(y-1=1;x-1=1\) hoặc \(y-1=-1;x-1=-1\)
\(x;y\) có 2 cặp: \(y=2;x=2\) hoặc \(y=0;x=0\)
9 tháng 4 2023
\(x\cdot\left(y-1\right)+y=2\\ xy-x+y=2\\ y\cdot\left(x+1\right)-x-1=2-1\\ y\cdot\left(x+1\right)-\left(x+1\right)=1\\ \left(x+1\right)\left(y-1\right)=1\)
mà `x;y in ZZ => x+1;y-1 in ZZ`
nên `x+1;y-1` thuộc ước nguyên của `1`
`=>x+1;y-1 in {1;-1}`
`=>x in {0;-2}; y in {2;0}`
TQ
0
H
1
NV
18 tháng 3 2023
\(x^2-3xy+2=y\)
\(\Rightarrow x^2+2=y\left(3x+1\right)\left(1\right)\)
\(\Rightarrow\left(x^2+2\right)⋮\left(3x+1\right)\)
\(\Rightarrow\left(9x^2+18\right)⋮\left(3x+1\right)\)
\(\Rightarrow\left[\left(9x^2-1\right)+19\right]⋮\left(3x+1\right)\)
Ta có \(9x^2-1=\left(3x+1\right)\left(3x-1\right)⋮\left(3x+1\right)\)
\(\Rightarrow19⋮\left(3x+1\right)\) nên \(3x+1\inƯ\left(19\right)\)
Lập bảng:
| 3x+1 | 19 | 1 | -19 | -1 |
| x | 6 | 0 | \(\dfrac{-20}{3}\left(l\right)\) | \(\dfrac{-2}{3}\left(l\right)\) |
Với \(x=6\). (1) \(\Rightarrow y=\dfrac{x^2+2}{3x+1}=\dfrac{6^2+2}{3.6+1}=2\)
Với \(x=0\). (1) \(\Rightarrow y=\dfrac{x^2+2}{3x+1}=\dfrac{0^2+2}{3.0+1}=2\)
Vậy các cặp số (x;y) thỏa điều kiện ở đề bài là \(\left(6;2\right),\left(0;2\right)\)
PD
2
XO
10 tháng 1 2023
Ta có : \(2^{x+1}.3^y=12^x\)
\(\Leftrightarrow3^y=\dfrac{12^x}{2^{x+1}}=\dfrac{3^x.4^x}{2^{x+1}}=\dfrac{3^x.2^{2x}}{2^{x+1}}=3^x.2^{2x}:2^{x+1}=3^x.2^{x-1}\)
\(\Leftrightarrow\dfrac{3^y}{3^x}=2^{x-1}\)
\(\Leftrightarrow3^{y-x}=2^{x-1}\)
\(\Leftrightarrow\left\{{}\begin{matrix}y-x=0\\x-1=0\end{matrix}\right.\Leftrightarrow x=y=1\)(tm)
Vậy (x;y) = (1;1) nghiệm của phương trình trên
T
1
x = 0 và y = 5
ngoc tan ơi ban có thể giải rõ ra cho mình được ko ạ