Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM: a) Xét t/giác ABM và t/giác ACM
có AB = AC (gt)
BM = MC (gt)
AM : chung
=> t/giác ABM = t/giác ACM (c.c.c)
b) Ta có: t/giác ABM = t/giác ACM (cmt)
=> góc AMB = góc AMC (hai góc tương ứng)
Mà \(\widehat{AMB}+\widehat{AMC}=180^0\)
=> \(2\widehat{AMB}=180^0\)
=> \(\widehat{AMB}=180^0:2=90^0\)
=> AM \(\perp\)BC ( Đpcm)
c) Xét t/giác AMD và t/giác CED
có AD = CD (gt)
góc ADM = góc EDC (đối đỉnh)
DM = DE (gt)
=> t/giác AMD = t/giác CED (c.g.c)
=> góc MAD = góc DCE (hai góc tương ứng)
Mà góc MAD và góc DCE ở vị trí so le trong
=> AM // EC (Đpcm)
d) Ta có : t/giác MAD = t/giác DCE (cmt)
=> AM = CE (hai cạnh tương ứng)
Do AM // EC (cmt) => góc AMC + góc MCE = 1800 (trong cùng phía)
=> góc MCE = 1800 - góc AMC = 1800 - 900 = 900 (vì góc AMB = góc AMC mà góc AMB = 900 => góc AMC = 900)
Xét t/giác AMC và t/giác MCE
có AM = CE (cmt)
góc AMC = góc MCE (cmt)
MC : chung
=> t/giác AMC = t/giác MCE (c.g.c)
=> ME = AC (hai cạnh tương ứng)
mà MD = DE = ME/2
hay AC/2 = MD (Đpcm)
a) Do M là trung điểm của BC (gt)
⇒ BM = MC
Do M là trung điểm của AD (gt)
⇒ AM = MD
Xét ∆ABM và ∆DCM có:
AM = MD (cmt)
∠AMB = ∠CMD (đối đỉnh)
BM = MC (cmt)
⇒ ∆ABM = ∆DCM (c-g-c)
b) Do ∆ABM = ∆DCM (cmt)
⇒ ∠ABM = ∠CDM (hai góc tương ứng)
Mà ∠ABM và ∠CDM là hai góc so le trong
⇒ AB // CD
c) Do AB // CD (cmt)
⇒ ∠CAE = ∠ACD (so le trong)
∠ACE = ∠CAD (so le trong)
Xét ∆ACE và ∆CAD có:
∠ACE = ∠CAD (cmt)
AC là cạnh chung
∠CAE = ∠ACD (cmt)
⇒ ∆ACE = ∆CAD (g-c-g)
⇒ AE = CD (hai cạnh tương ứng)
Do ∆ABM = ∆DCM (cmt)
⇒ AB = CD (hai cạnh tương ứng)
Mà AE = CD (cmt)
⇒ AB = AE
Vậy A là trung điểm của BE
a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó: ΔABM=ΔACM
b: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
c: Xét tứ giác ABMH có
I là trung điểm của AM
I là trung điểm của BH
Do đó: ABMH là hình bình hành
Suy ra; AH//BM
hay AH//BC
a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó: ΔABM=ΔACM
b: Ta có: DB+AD=AB
EC+AE=AC
mà AD=AE
và AB=AC
nên DB=EC
Xét ΔDBM và ΔECM có
DB=EC
\(\widehat{B}=\widehat{C}\)
MB=MC
Do đó: ΔDBM=ΔECM
Suy ra: MD=ME
Ta có: AD=AE
nên A nằm trên đường trung trực của DE(1)
ta có: MD=ME
nên M nằm trên đường trung trực của DE(2)
Ta có: AB=AC
nên A nằm trên đường trung trực của BC(3)
Ta có: MB=MC
nên M nằm trên đường trung trực của BC(4)
Từ (1) và (2) suy ra AM là đường trung trực của DE
hay AM\(\perp\)DE
Từ (3) và (4) suy ra AM là đường trung trực của BC
hay AM\(\perp\)BC
a: Xét ΔMAB và ΔMEC có
MA=ME
góc AMB=góc EMC
MB=MC
=>ΔMAB=ΔMEC
b: ΔMAB=ΔMEC
=>góc MAB=góc MEC
=>AB//CE
c: Xét ΔMHA vuông tại H và ΔMKE vuông tại K có
MA=ME
góc HAM=góc KEA
=>ΔMHA=ΔMKE
=>MH=MK
=>M là trung điểm của HK
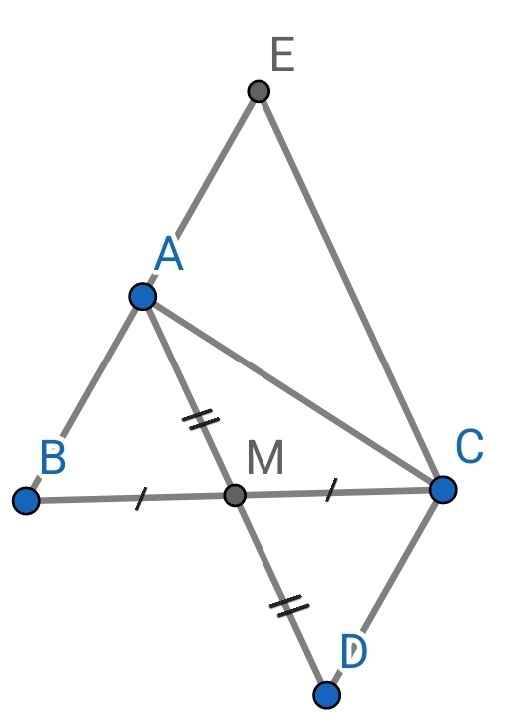
a/ \(\Delta ABM\)và \(\Delta ACM\)có: AB = AC (gt)
Cạnh AM chung
BM = MC (M là trung điểm của BC)
=> \(\Delta ABM\)= \(\Delta ACM\)(c. c. c) (đpcm)
b) \(\Delta ABM\)và \(\Delta ECM\)có:
BM = CM (M là trung điểm của BC)
\(\widehat{AMB}=\widehat{EMC}\)(đối đỉnh)
AM = EM (gt)
=> \(\Delta ABM\)= \(\Delta ECM\)(c. g. c) (đpcm)
c) Ta có \(\Delta ABM\)= \(\Delta ACM\)(cm câu a) => \(\widehat{AMB}=\widehat{AMC}\)(hai góc tương ứng)
và \(\widehat{AMB}=\widehat{EMC}\)(đối đỉnh)
=> \(\widehat{AMC}=\widehat{EMC}\)
\(\Delta ACM\)và \(\Delta ECM\)có: Cạnh MC chung
\(\widehat{AMC}=\widehat{EMC}\)(cm trên)
AM = EM (gt)
=> \(\Delta ACM\)= \(\Delta ECM\)(c. g. c)
=> \(\widehat{ACM}=\widehat{ECM}\)(hai góc tương ứng)
=> CB là tia phân giác của \(\widehat{C}\)(đpcm)
a) xét tam giác ABM và tam giác ACM
có: AB = AC (giả thiết)
BM =CM(giả thiết)
AM chung
do đó tam giác ABM = tam giác ACM(c-c-c)
b)xét tam giác ABM và tam giác ECM
Có: BM =CM (gt)
góc AMB = góc EMC(2 góc đối đỉnh)
AM = EM(gt)
do đó tam giác ABM = tam giác ACM(c-g-c)
suy ra góc ECM = góc ABM(hai góc tương ứng)
mà góc ECM và góc ABM là hai góc so le trong
suy ra EC song song với AB(điều cần chứng minh)
c)VÌ tam giác ABM = tam giác ACM(chứng minh trên) và tam giac ABM cũng = tam giác ECM
nên tam giác ACM = tam giác ECM
suy ra:góc ACM = góc ECM (hai góc tương ứng)
suy ra :CB là tia phân giác của góc C