Hãy chứng tỏ rằng diện tích 4 cánh hoa thị trên hình 26 bằng tổng diện tích các phần kẻ ngang.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Hình của bài như thế này phải không ? Nếu như thế thì mk giải cho ! Bài này cô mk dạy rồi !
Phân tích : Vì BP = \(\frac{1}{3}\)BC và hai hình tam giác : ABP và ABC có chung chiều cao hạ từ đỉnh A xuống đáy BC nên diện tích tam giác ABP bằng \(\frac{1}{3}\)diện tích tam giác ABC.
Tượng tự,diện tích mỗi hình tam giác BCM và CAN cũng bằng \(\frac{1}{3}\)diện tích tam giác ABC.
Vậy tổng diện tích ba tam giác : ABP , BMC , CAN bằng diện tích tam giác ABC.
Về mặt lý thuyết thì chúng có thể phủ kín tam giác ABC . Nhưng thật ra chúng để thừa lại phần diện tích tam giác IEF và chũng lại phủ lên các tam giác: IMC , EAN , FBP mỗi tam giác phủ hai lần nên thừ ra một lần . Chính điều này chứng tỏ :
SFBP + SEAN + SIMC = SIEF
Chúc bạn hok tốt !
A B C M N E I F

Gọi đường chéo của hình MNPQ là a
Theo bài ra ta có: S của ABCD =a.a (Vì đường chéo của MNPQ = cạnh của ABCD), S của MNPQ =(a.a):2
Mà a.a:((a.a):2)=SABCD : SMNPW =1/2 .Suy ra SMNPQ =1/2 SABCD
Gọi đường chéo của hình MNPQ là a
Theo bài ra ta có: S của ABCD =a.a (Vì đường chéo của MNPQ = cạnh của ABCD), S của MNPQ =(a.a):2
Mà a.a:((a.a):2)=SABCD : SMNPW =1/2 .Suy ra SMNPQ =1/2 SABCD

Giải thích các bước giải:
Bài làm
Trong ΔABC, ta có: D là trung điểm BC
ED = 1/2 AE
⇒E là trọng tâm của ΔABC
Mà BE cắt AC tại G
⇒G cũng là trung điểm của AC.
Giải thích các bước giải:
Bài làm
Trong ΔABC, ta có: D là trung điểm BC
ED = 1/2 AE
⇒E là trọng tâm của ΔABC
Mà BE cắt AC tại G
⇒G cũng là trung điểm của AC.

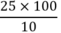 =2500
(
m
2
)
=2500
(
m
2
)
Chịu! Có hình đâu?
dung co hinh dau